1
Организация данных. Создание рабочей таблицы.
Сначала займемся организацией данных и создадим рабочую таблицу.Распределительный центр работает каждый день, 7 дней в неделю. Поэтому добавим к таблице с данными задачи 7 столбцов (по числу дней недели).
- Для планирования поставок нам потребуется 7х25 двоичных переменных:
-
1 - поставка есть; -
0 - поставки нет.
Закрасим поле переменных желтым цветом .
оптимально расставить единицы в желтом поле переменных
Для того, чтобы убедиться, что единички в желтом поле переменных расставлены в нужном количестве, добавим столбец
Внизу таблицы в голубых ячейках будем вычислять ежедневную суммарную нагрузку распределительного центра, т.е. число единиц, которое склад собирает и отгружает ежедневно.
-
Однако, чтобы вычислить ежедневную нагрузку склада, необходимо знать, сколько единиц товара содержится в одной поставке для
каждого магазина. Для этого:
- добавим новый столбец Величина одной поставки, ед.;
- в каждую ячейку нового столбца введем формулу:
Ожидаемые продажи, ед. / Плановое число поставок (для каждой торговой точки)
С чем мы можем сравнить найденные ежедневные нагрузки распределительного центра?
Очевидно, что с его среднедневной нагрузкой.
Мы знаем, что сумма ожидаемых продаж всех торговых точек за неделю есть суммарное количество единиц, которое распределительный центр должен собрать и отгрузить за неделю.
Вычислим среднюю нагрузку распределительного центра за день.
- Для этого:
- Сумму ожидаемых продаж по всем торговым точкам разделим на
7 . - Окрасим ячейку, в которой вычисляем среднюю дневную нагрузку распределительного центра в светло-оранжевый цвет .
Здесь та же таблица в файле MS Excel с соответствующими формулами:
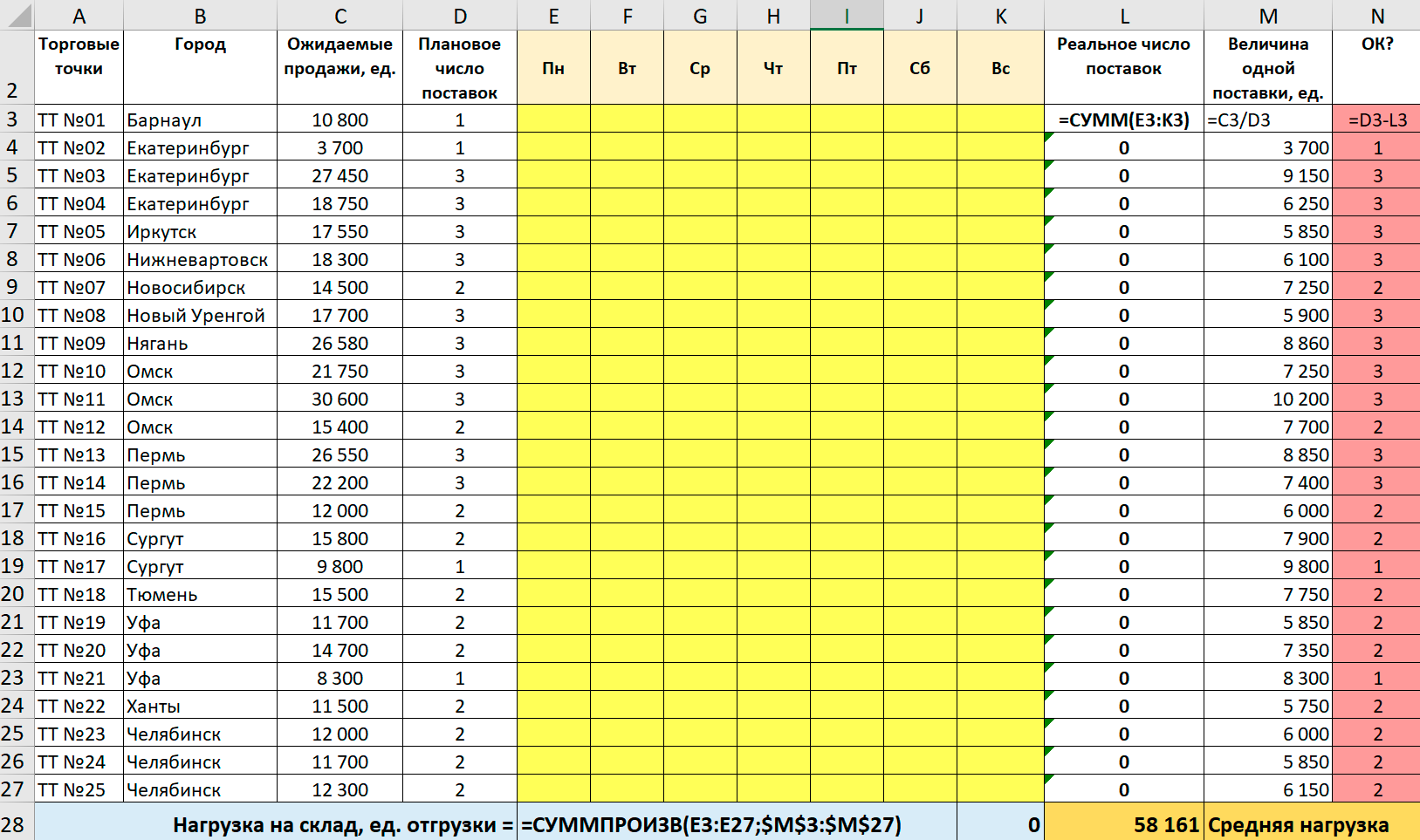
Для удобства визуального контроля в столбец
2
Как измерять неравномерность (разброс) в нагрузке?
Поскольку мы должны составить план поставок таким образом, чтобы нагрузка на распределительный центр была равномерной, то возникает вопрос: как имерить неравномерность нагрузки?Для вычисления дисперсии считаются квадраты отклонения нагрузки от средней, а для вычисления стандартного отклонения и вовсе корень квадратный из дисперсии. А нелинейности следует избегать до последней возможности, поскольку нелинейная оптимизация гораздо более сложна, чем линейная.
Что же можно использовать в качестве линейной характеристики разброса?
По идее, лучше всего подошла бы разница между минимальной и максимальной загрузками распределительного центра. Вот только использовать функции Excel
Допустим, например, что загрузка должна быть максимальной в понедельник и минимальной в воскресенье. По идее это выглядит очень гуманно.
Если мы потребуем этого в условиях задачи, то разброс нагрузки можно будет вычислить просто как разницу нагрузок в понедельник и воскресенье.
- Дополним нашу таблицу еще одним полем:
- назовем это поле Разброс =;
- в зеленой
ячейке вычислим этот разброс:
вычтем из суммарной нагрузки склада в понедельник суммарную нагрзку склада в воскресенье,
т.е. из значения светло-голубой ячейки0столбцаПн вычтем значение светло-глубой ячейки0столбцаВс
Теперь рабочая таблица готова, осталось только поставить задачу оптимизатору.
3
Установки оптимизатора.
Задача наша небольшая, всего 175 переменных, поэтому по силам даже штатному Поиску решения.- Введем данные задачи в оптимизатор:
- Целевая функция в данной задаче – разброс нагрузки распределительного центра, который вычисляется в зеленой ячейке.
- Мы хотим, чтобы нагрузка на распределительный центр была по возможности равномерной. Поэтому потребуем, чтобы значение целевой функции было минимальным.
- Переменные нашей задачи - это все желтое поле в рабочей таблице.
- Введем ограничения:
- поскольку мы волевым образом решили, что самая большая нагрузка приходится на понедельник,
то нагрузка на склад в кажый следующий день, должна быть не больше нагрузки предыдущего дня:
$E$28:$J$28 >= $F$28:$K$28 -
Переменные должны быть бинарными:
$E$3:$K$27 = бинарное - Значения контрольного столбца
OK? должны быть равны 0, что означает: число плановых поставок в каждую торговую точку равно числу реальных поставок в эту торговую точку.
$N$3:$N$27 = 0
- поскольку мы волевым образом решили, что самая большая нагрузка приходится на понедельник,
то нагрузка на склад в кажый следующий день, должна быть не больше нагрузки предыдущего дня:

Запустим задачу, и ...
Поиск решения ищет оптимальное решение столько времени, что не хватает терпения дождаться результата!
Хм... Может быть Поиск решения излишне упрощен?Попробуем OpenSolver с солвером CBC.
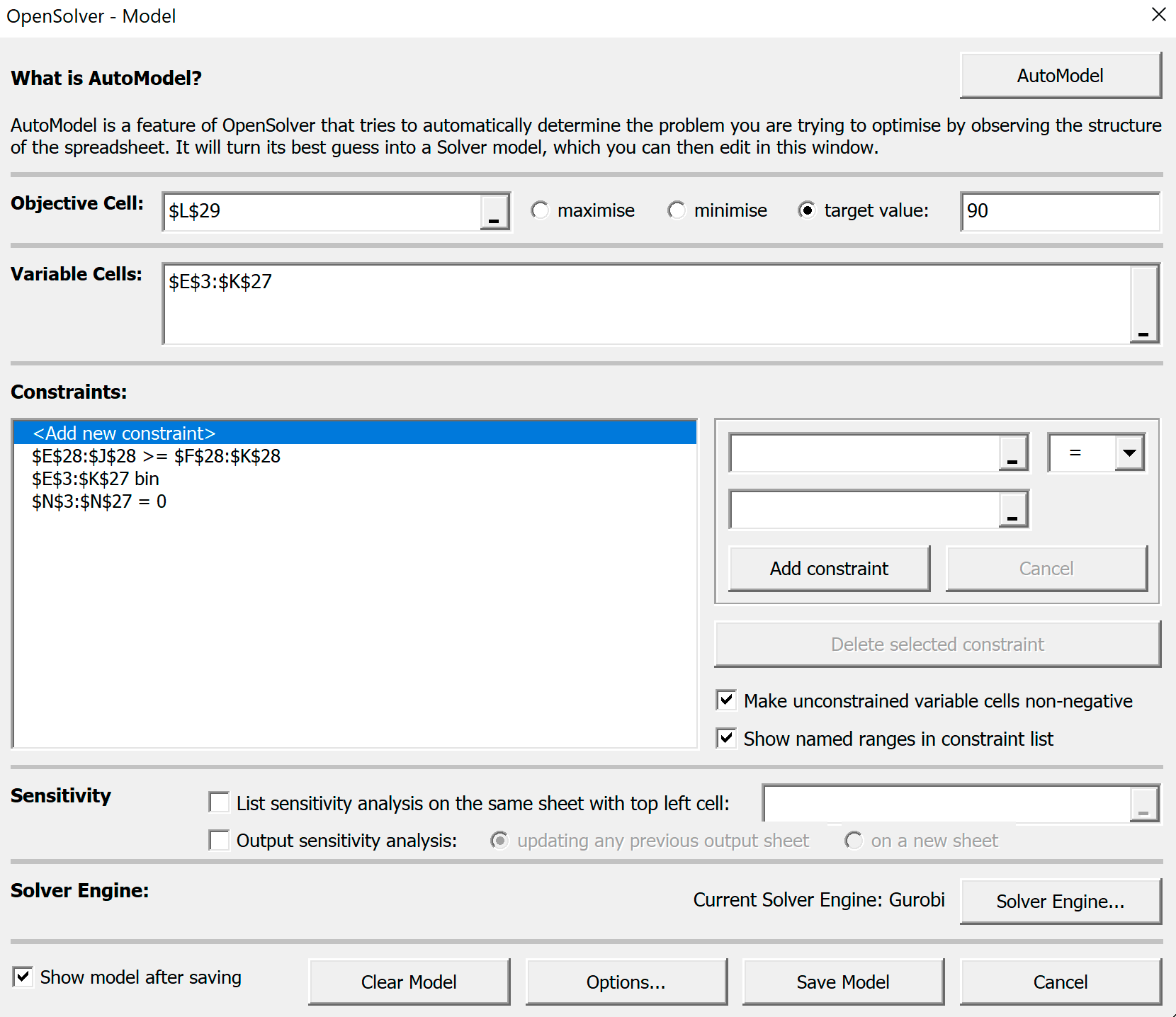
Перенесем настройки оптимизатора в OpenSolver-Model:
Запустим задачу, и ...
Как ни странно, но здесь процесс тоже продолжается до бесконечности (во всяком случае дольше 12 часов)...
Еще более странно, что солвер от Gurobi тоже не может быстро выдать оптимальное решение и считает неопределенно долго (мне не хватило терпения дождаться результата).
4
Как выяснить, что пошло не так и все-таки решить задачу.
В меню Options установок OpenSolver OpenSolver-Model есть пункт Show optimization progress while solving.
Если его отметить, то по ходу оптимизации будет показываться дополнительное окно с промежуточными результатами.
И тут мы можем видеть камень преткновения. Оптимизатор уже через 10 секунд (числа в правой колонке: 10s) достигает разброса 550 ед, что составляет примерно 1% от средней нагрузки распределительного центра, через 30 секунд доходит до варианта с разбросом 90 ед. и… продолжает процесс поиска дальше и дальше...и через 1000 секунд оптимизатор продолжает пережевывать варианты размещения поставок с одним и тем же разбросом 90…
С другой стороны, раз мы видели, что OpenSolver получает нужный нам результат и даже с запасом, но почему-то им не удовлетворяется, мы можем сами поставить ограничение на результат.
Применим опцию
Оптимизатор от Gurobi получает оптимальное решение примерно за 60 секунд.
Если мы зададим, например,
Можно обойти это неудобство оставив целью оптимизации минимум, но добавив ограничение на целевую функцию:

Оптимизатор от Gurobi получает оптимальное решение с разбросом 100 за 92 сек.
Но нужно ли запрашивать такую точность? При средней нагрузке около 58 000 и допустимой неравномерности в 1% предел оптимизации можно было бы поставить равным 580.
С практической точки зрения и 5%-ная разница в нагрузке будет весьма мало заметна, так что смело можно было бы поставить в качестве предела и 2-3 тыс. Задачу при подобном ограничении солвер COIN-OR CBC решает менее чем за полминуты.
Итак, модель решения задачи планирования поставок с учетом равномерной нагрузки распределительного центра построена. Теперь оценим качество полученного решения и по возможности улучшим его.
5
Как учесть равномерность поставок.
Внимательно изучив полученное решение, мы сочтем его не самым оптимальным. Равномерность поставок оставляет желать лучшего. Так например, в ТТ №11 в Омске предлагается все три поставки собирать и отправлять одну за другой три дня подряд. В то время, как было бы гораздо разумнее, получать их через день.Как задать ограничение на равномерность поставок?
В общем виде это сделать не просто, необходимо иметь дополнительные конкретные данные. Но для примера можно предложить следующий вариант решения этой проблемы.
Создадим такую контольную таблицу размером 7х25. В каждую ячейку контрольной таблицы введем формулу, вычисляющую сумму поставок за два дня: сегодняшний и предыдущий. И не забудем, для понедельника предыдущим днем будет воскресенье.
В файле MS Excel таблица с формулами выглядит так:

Условным форматированием в контрольной таблице выделены ячейки, отличные от 1.
- Обновим настройки OpenSolver-Model. Добавим условие
- значение всех ячеек контрольной таблицы должны быть не больше 1:
$P$3:$V$27 <=1

После запуска OpenSolver получим новое решение:

мы задаем одинаковые требования для промежутков между поставками при любом числе поставок в неделю.
- По смыслу,
- при одной поставке в неделю контролировать интервалы нет смысла вообще.
- при двух поставках в неделю лучше бы задать интервалы не меньше 2 дней.
- при трех поставках в неделю интервал в один день подходит.
- если число поставок больше трех, нужно формулировать новые требования для дней поставок.
- Для учета этих требований имеет смысл:
- Oтсортировать торговые точки по числу поставок.
- В контрольной таблице визуально выдлить области, соответствующие поставкам 1 раз в неделю, 2 раза в неделю и 3 раза в неделю.
- В зонах с 1 и 3 поставками в неделю формулы менять не нужно.
- В контрольной таблице в зоне с 2 поставками в неделю формулы нужно откорректировать.
- Как изменить формулы в контрольной таблице в зоне с 2 поставками?
- необходимо вычислить сумму числа поставой за сегодняшний и два предыдущих дня.
- Для понедельника нужно находить суммы числа поставок за субботу, воскресенье и понедельник.
- Для вторника нужно находить суммы числа поставок за воскресенье, понедельник и вторник.
Для этого:
- Теперь остается откорректировать ограничение в OpenSolver:
- вместо P3:V27<=1 достаточно требовать P7:V27<=1. То есть, не накладывать ограничений на зону с 1 потавкой в неделю.
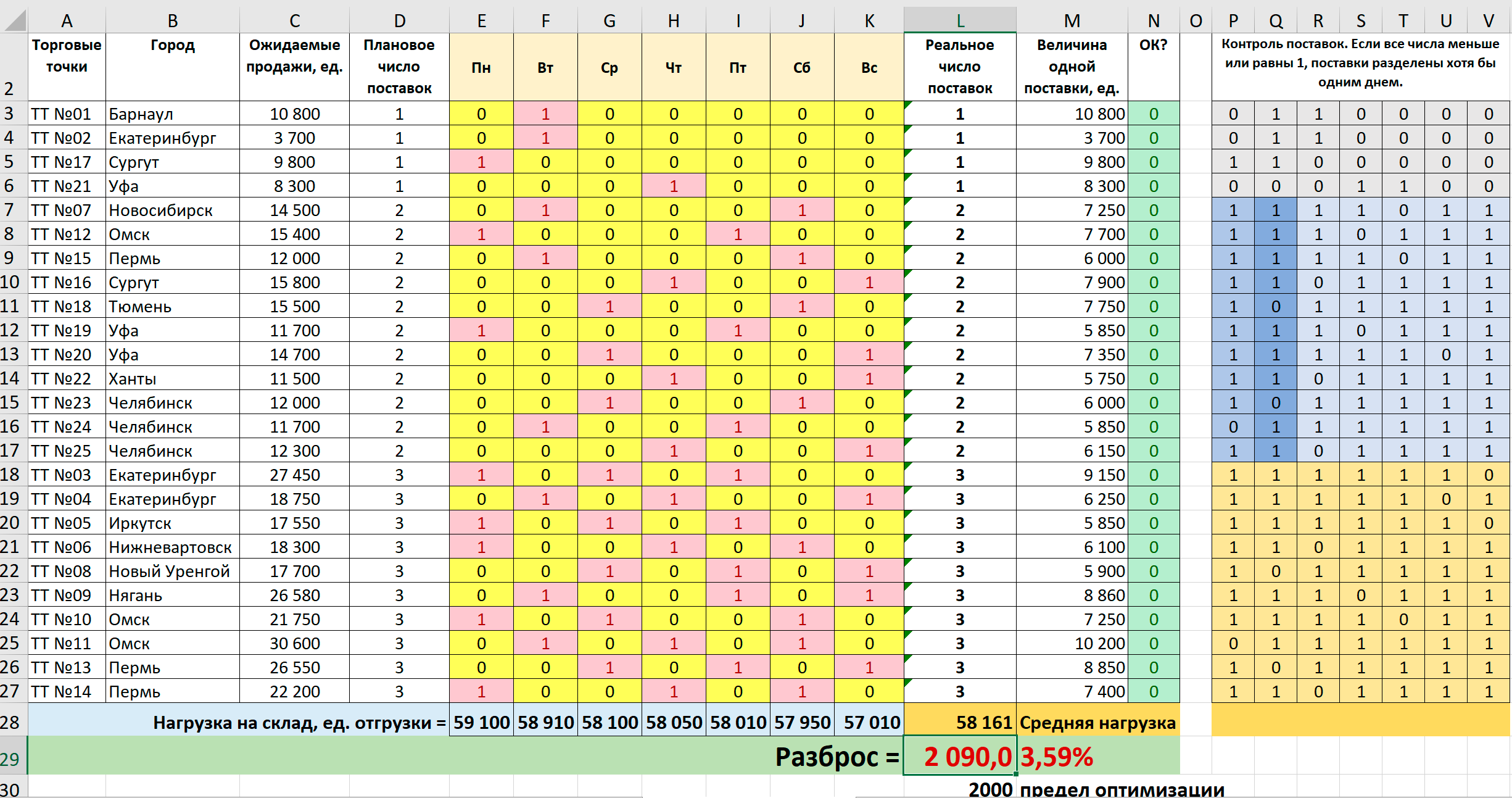 Разумеется, разброс загрузки распределительного центра несколько увеличился, но все равно остался очень маленьким.
Разумеется, разброс загрузки распределительного центра несколько увеличился, но все равно остался очень маленьким.
Как запретить поставки в определенные дни?
Cоответствующая переменная в желтом поле таблицы переменных должна быть равна 0 в установках OpenSolver-Model
Как потребовать поставку в определенный день?
Cоответствующая переменная в желтом поле таблицы переменных должна быть равна 1 в установках OpenSolver-Model
 Скачать файл "delivery_schedule.xlsx" (примерно 59 Кб)
Скачать файл "delivery_schedule.xlsx" (примерно 59 Кб)