Будем рассматривать решение этой задачи на базе тех знаний и допущений, которые мы обсуждали на странице Построй маршрут.
Все пункты расположены на участке размером 20х20 км.
1
Таблица расстояний задачи построения маршрута для двух мусоровозов.
Примем, что мусоровозы выезжают из одного и того же пункта – с точки зрения практической ситуации это вполне реалистическое предположение. Для этого совместим пункты п01 и п02 по координатам: оба пункта будут располагаться в точке (Расстояния между
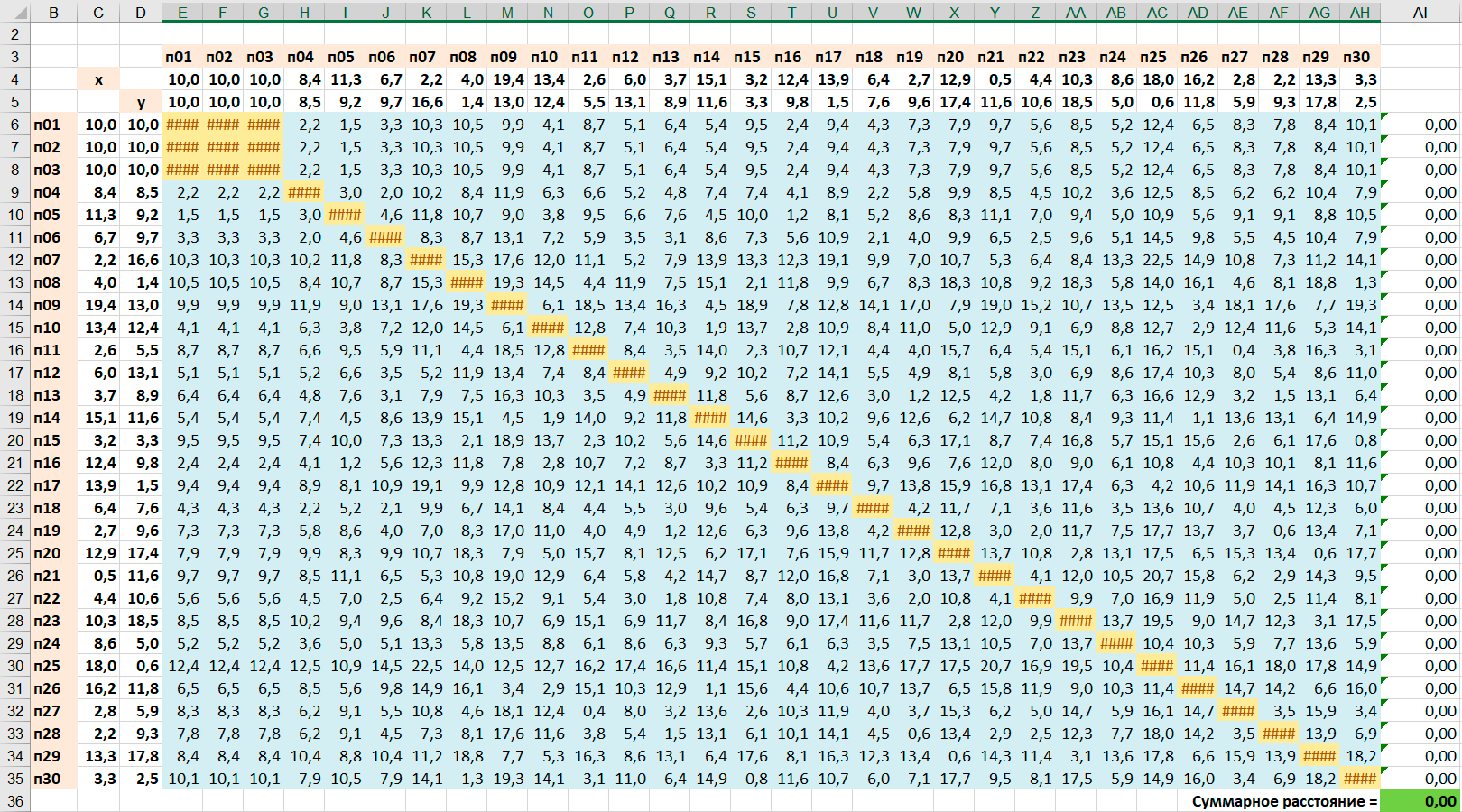
Создадим Таблицу расстояний для решения задачи.
Для этого смоделируем координаты 22 точек посещения датчиком случайных чисел и вычислим расстояния между этими точками посещения.
Получим примерно такую Таблицу расстояний:Для этого смоделируем координаты 22 точек посещения датчиком случайных чисел и вычислим расстояния между этими точками посещения.
2
Таблица переменных задачи построения маршрутов двух мусоровозов.
Таблица переменных будет такой же, как мы рассматривали ранее- Напомню:
- Желтое поле - ячейки и оранжевые ячейки - это область переменных. Именно эти ячейки мы будем указывать в качестве переменных в установках OpenSolver
- Значения оранжевых ячеек -
при решении задачи всегда будут равны
0 .
3
Таблица специальных ограничений для решения задачи о нахождении маршрутов двух мусоровозов.
Подготовим стандартную таблицу специальных ограничений.- Замечания к таблице специальных ограничений:
- Желтый столбец Таблицы специальных ограничений - ячейки - это переменные, которые показывают порядок посещения пунктов маршрута - от
- второй подмаршрут начнется из точки
n02 . Поэтому, если точкаn02 окажется в середине общего маршрута, ее номер посещения будет 11 или около того. - Используя соображение, сформулированное в предыдущем пункте, зададим нижнюю и верхнюю границы для номера посещения
n02 :
min=10 иmax=12
В этом случае состав маршрутов будет различаться не более чем на 1-2 пункта.
Таким образом, мы хотим найти два оптимальных маршрута между точками забора мусора:
4
Ограничения, которые необходимо задать для решения задачи о нахождении маршрутов двух мусоровозов.
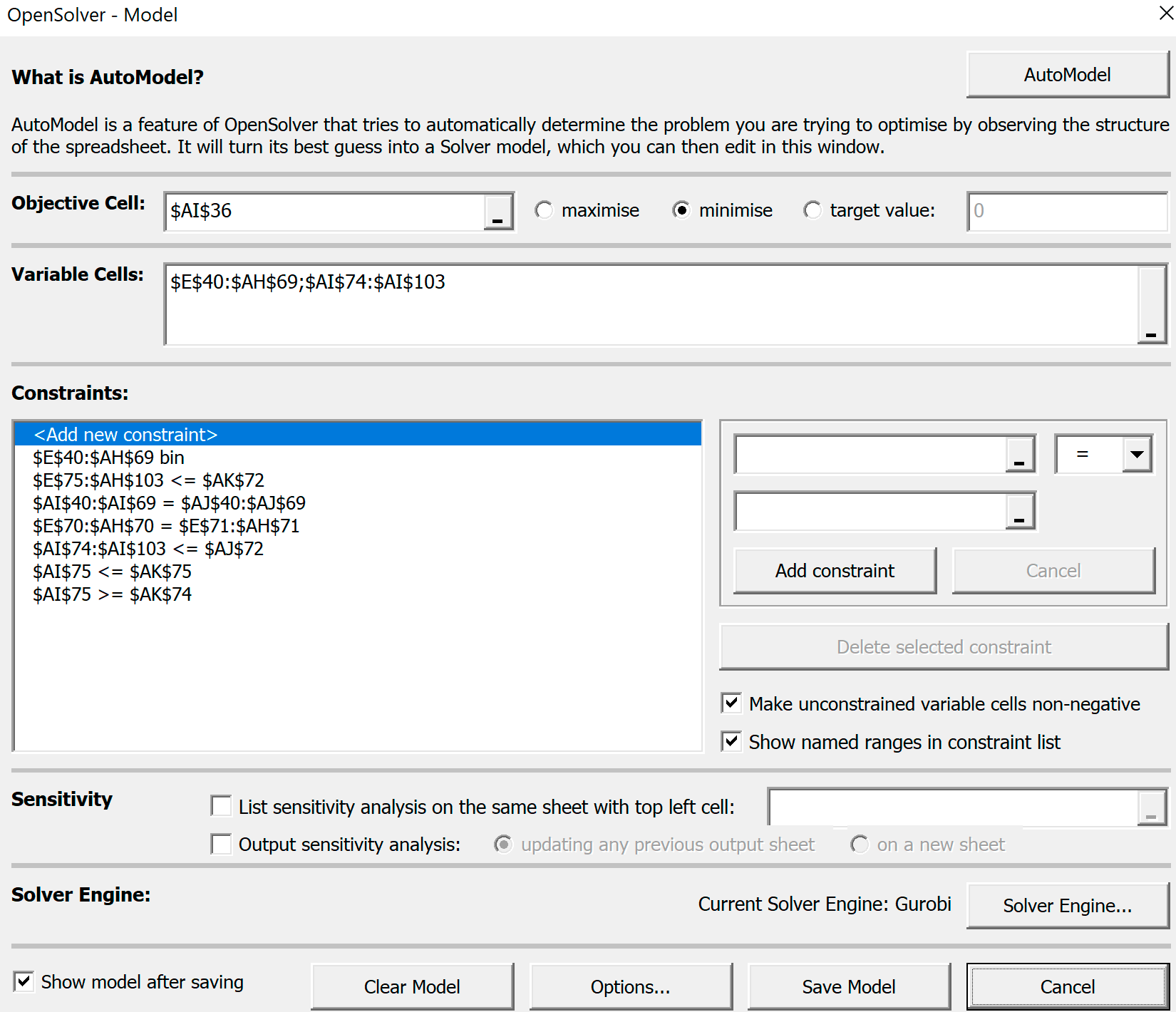
Теперь все готово для решения задачи. Будем искать оптимальное решение с помощью OpenSolver.- Введем данные и ограничения в OpenSolver - Model:
- цель по-прежнему: найти самый короткий маршрут - значение ячейки
$AB$29 должно быть минимальным; - все те же переменные в задаче - желтые ячейки в таблице переменных и желтые ячейки в таблице специальных ограничений
$E$33:$AA$55 ;$AB$60:$AB$82 - ограничения задачи:
- переменные из таблицы переменных должны быть бинарными (принимать значение
0 или1 -
$E$33:$AA$55 bin - суммы выездов из пунктов посещения и суммы въездов в каждый из них равны заданному числу -
$AB$33:$AB$55 = $AC$33:$AC$55
$E$56:$AA$56 = $E$57:$AA$57 - точка
n02 должна быть в середине общего маршрута:
$AB$61 >= $AD$60
$AB$61 <= $AD$61 - условие, запрещающее короткие циклы
$E$61:$AA$82 <= $AD$58 - ограничим переменные
AB60:AB82 сверху
$AB$60:$AB$82 <= $AC$58 .
Если этого не сделать, то оптимизатор найдет решение для одного связного маршрута: начнет отсчет от точкиn02 , присвоив ей значение, например, 10, а остальные номера будет отсчитывать от этого значения так, что последняя точка посещения будет иметь номер 33.
- переменные из таблицы переменных должны быть бинарными (принимать значение

5
Решение задачи оптимального маршрута для двух мусоровозов.
После запуска OpenSolver выдаст решение, вычислит суммарный маршрут 107,33 км, длины каждого подмаршрута при оптимизации в нашей модели не вычисляются: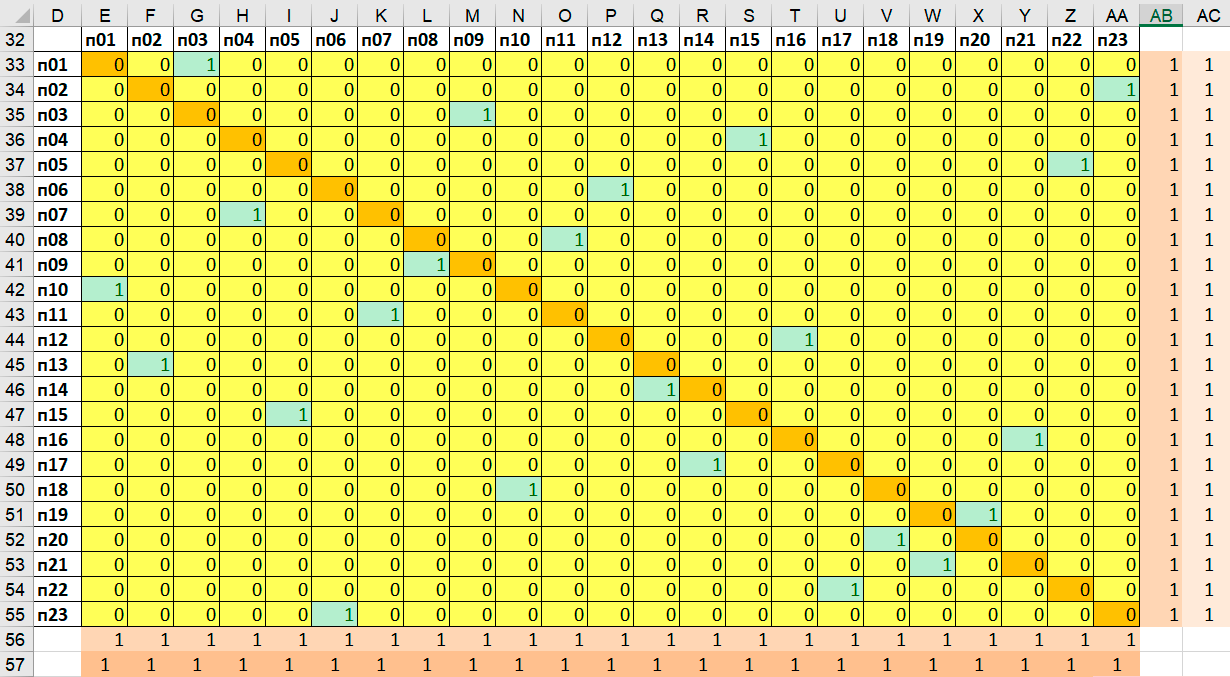
На карте решение выглядит так:
Для сравнения приведу маршрут, который получится, если убрать условие, что точка
На картинке с одиночным маршрутом из-за фактического запрета участка
6
Можно ли изменить решение задачи оптимального маршрута для двух мусоровозов?
В решении с двумя маршрутами номер пунктаOpenSolver находит решение, однако длительность поиска этого оптимального решения значительно возрастает.
Если для маршрута одной машины решение находится за 1 сек даже с умолчальным солвером CBC,
то первый маршрут на две машины оптимизируется 35 сек, а последний маршрут с более равными подмаршрутами требует уже более 35 минут расчетов.
При таких условиях подмаршруты меняются довольно радикально, при очень небольшом возрастании суммарной длины (107,68 км).
7
Оптимальный маршрут для трех мусоровозов.
В свете рассмотренного варианта с двумя машинами имеет смысл обсудить решения с тремя и более машинами, чтобы обобщить задачу.Рассмотрим вариант задачи из 28 пунктов посещения. Для решения использовался солвер от Gurobi, так как оптимизация получается более сложной.
Итак, используем сразу три совпадающих пункта
Таблица расстояний для задачи построения маршрутов трех мусоровозов:
 Подготовим таблицу переменных:
Подготовим таблицу переменных:
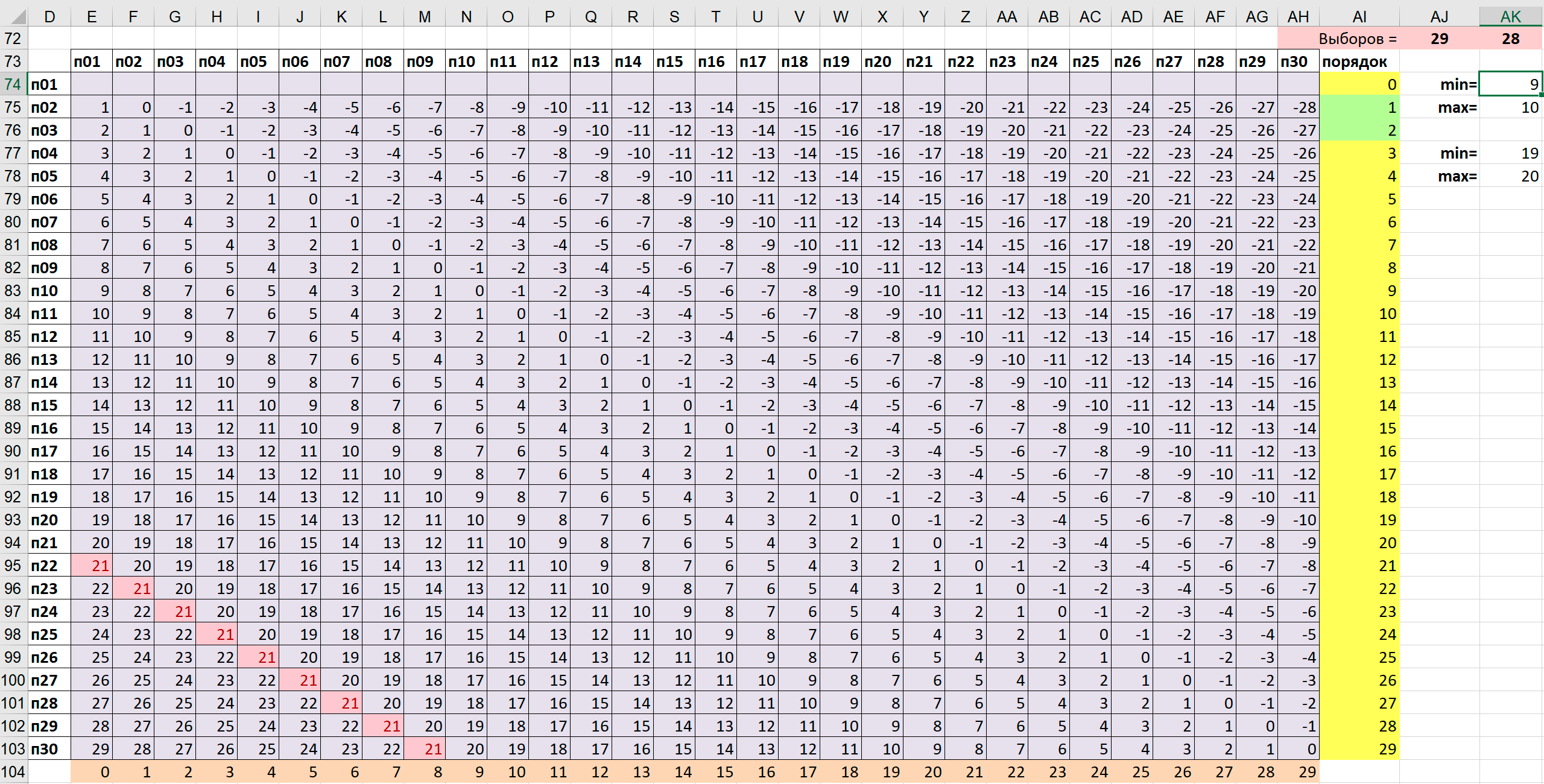
 Таблица специальных ограничений:
Таблица специальных ограничений:

 Подготовим таблицу переменных:
Подготовим таблицу переменных: Таблица специальных ограничений:
Таблица специальных ограничений:
Решение с одним маршрутом.
Для получения решения с одним маршрутом (в качестве маршрута сравнения) выключим пункты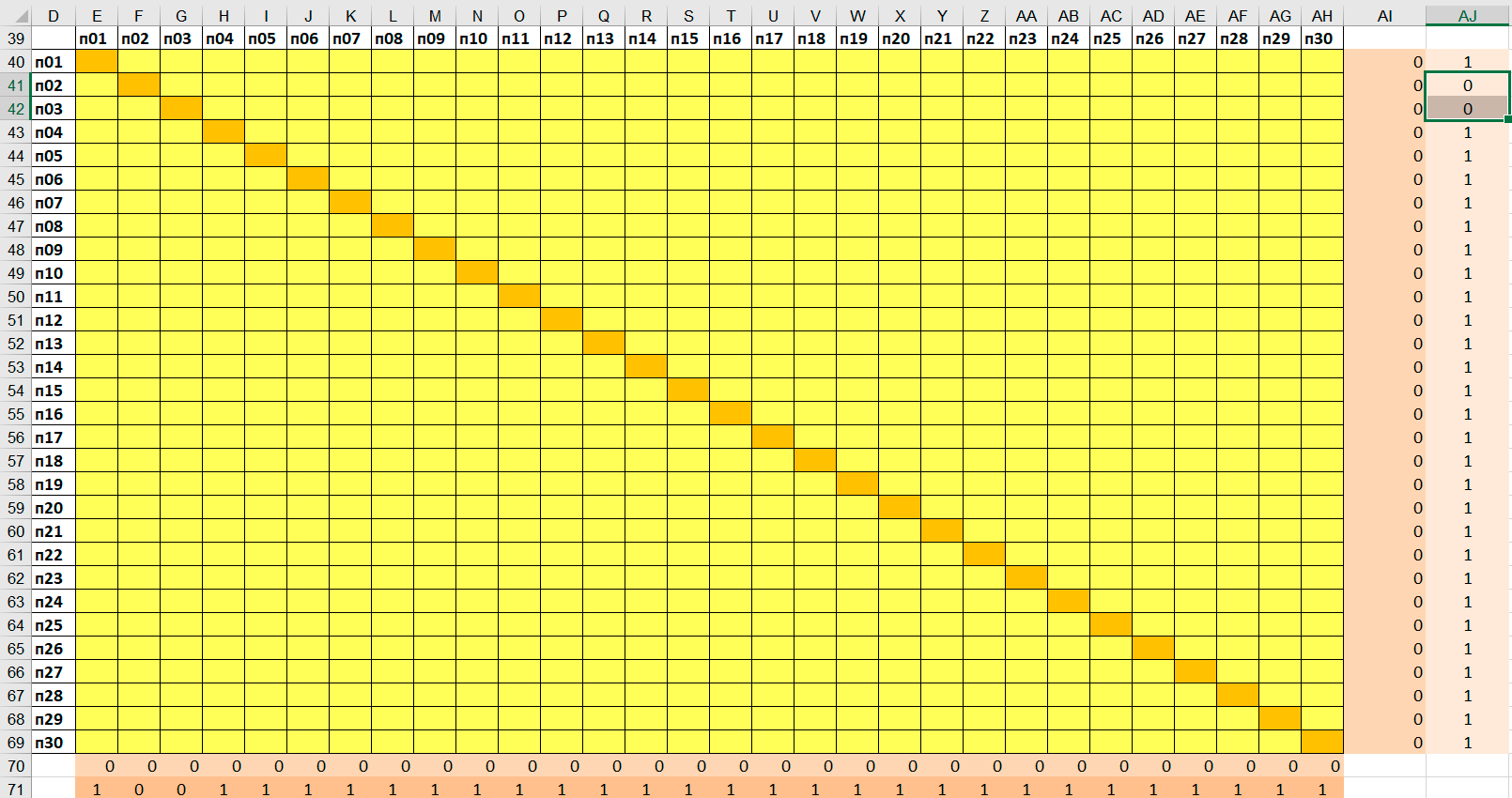
В установках OpenSolver ничего не меняем и для одиночного маршрута получаем следующее решение.
Длина найденного маршрута - 89,98 км
Решение с маршрутом для двух машин.
Для того, чтобы получить два маршрута, нужно включить пунктПусть точка


Добавляем в установки OpenSolver ограничения для
где и нижнюю и верхнюю границу для номера в очереди посещений пункта
Важно не забыть добавить требование, что все номера посещений не должны превышать
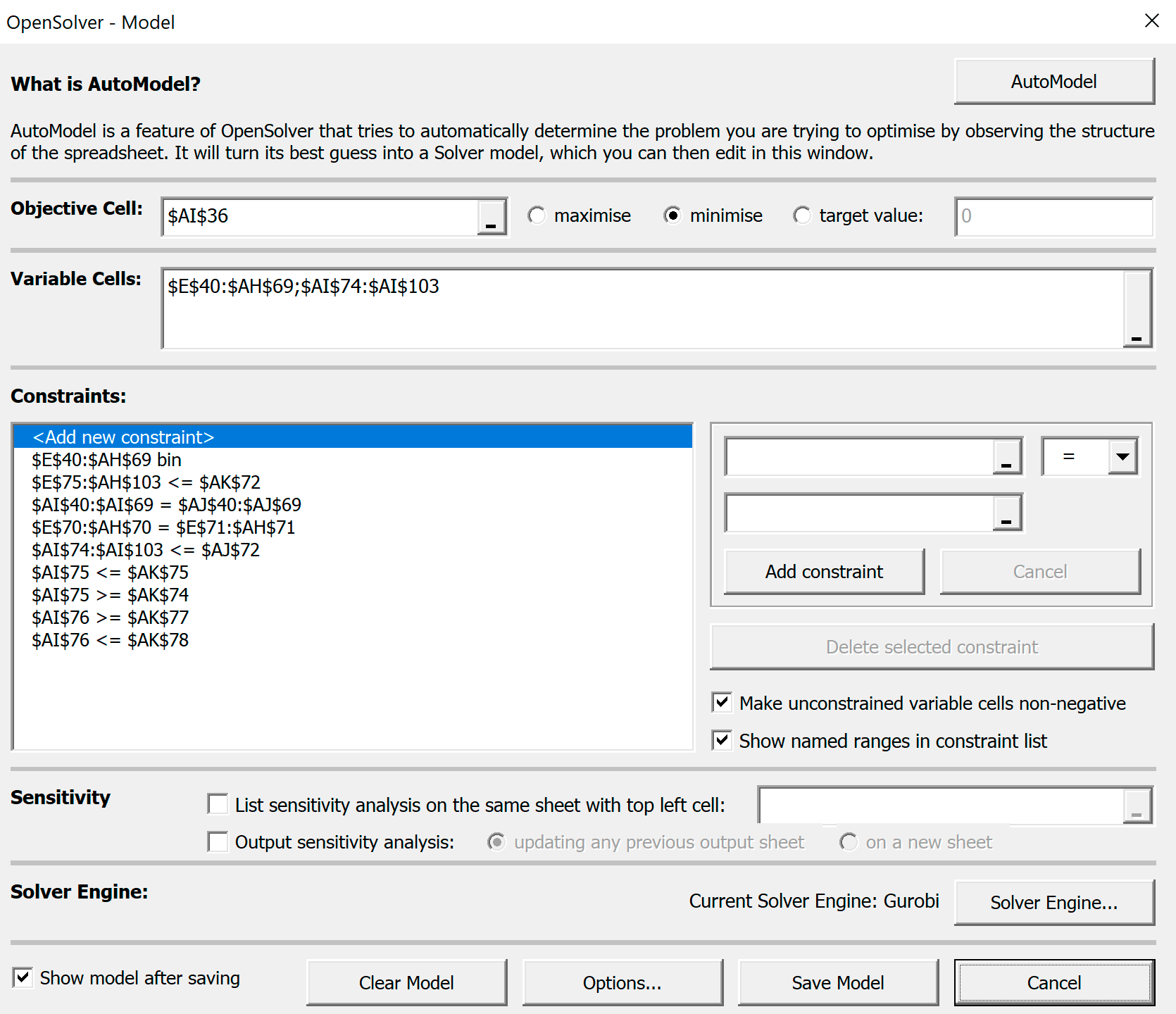
Установки OpenSolver-Model:
Тогда для двух вариантов решения задачи получим следующую картину:
Как и в предыдущих случаях суммарная длина маршрута подрастает от 89,98 км до 95,85км.
Если чуть ослабить ограничение на номер
Решение с маршрутом для трех машин.
Теперь модифицируем модель для получения варианта с тремя машинами.Во-первых, разрешим посещение и пункта
Для обоих пунктов
Заведомо ясно, что при равномерном распределении точек посещения по маршрутам номера посещения
Добавим ограничения в установки OpenSolver.
В результате оптимизации получим следующий вариант решения. Суммарная длина маршрута - 102,03км
Пусть
Получим новый маршрут, длина которого 101,16 км:
Таким образом, можно сформулировать следующий алгоритм решения проблемы с несколькими серверами, посещающими заданные пункты.
1. Дублируем исходный пункт столько раз, сколько у нас серверов минус 1.
2. Делим число пунктов посещения на число серверов для того, чтобы примерно определить районы поиска оптимальных номеров посещения всех дублирующих пунктов. Задаем минимальные и максимальные номера для каждого пункта в соответствии с допустимым отклонением нагрузки на серверы.
3. Требуем, чтобы все номера посещения в соответствующем столбце были не больше полного числа точек минус 1.
 Скачать файл "garbage_truck_route 4.xlsx" (примерно 442 Кб)
Скачать файл "garbage_truck_route 4.xlsx" (примерно 442 Кб)