Логотип HCXL Учтём вместимость машин
Рассматривая варианты решения множественных задач коммивояжера, мы должны не только рассмотеть вопрос о нескольских маршрутах, но и обсудить вопрос:
Что если вместимость машин ограничена, и они не могут обслужить все пункты посещения?
Задача возникает, когда необходимо развезти товар по торговым точкам, но его столько, что одного рейса недостаточно.


Здесь мы рассматриваем один из вариантов решения этой проблемы.
Машины выезжают из одного и того же пункта, чтобы доставить товар в некоторое количество точек и вернуться в начальный пункт.
Данные о расстояниях между каждой парой точек оценены по их координатам.
Данные о потребностях точек в товаре известны.
Требуется построить модель расчета кратчайшего маршрута посещения всех точек машинами с учетом их вместимости, так чтобы потребности точек в товаре были удовлетворены полностью.
Подход к решению этой задачи близок к решению задачи о построении кратчайшего маршрута для нескольких мусоровозов. Однако его приходится усложнить.
Для привязки пунктов посещения к конкретной машине придется добавить переменных. Потому что даже в самом простом случае с двумя машинами (и маршрутами) нам необходимо как-то выделить оба подмаршрута для расчета загрузки машин.
    Идея для новой переменной довольно проста:
  • один из подмаршрутов (маршрут одной машины) обозначим единицами;
  • второй подмаршрут обозначим нулями;
  • тогда перемножая этот набор переменных на потребности торговых точек в товаре получим загрузку первой машины, а на долю второй достанется остаток товара
Все пункты расположены на участке размером 20х20 км.

1

Решение задачи построения маршрута для двух машин и 28 точек посещения.

Примем, что две грузовые машины выезжают из одного и того же пункта, расположенного в центре района (X=10 и Y=10).
Для построения двух маршрутов совместим пункты n01 и n02 по координатам (X=10 и Y=10). Расстояния между n01 и n02 примем равным 10000, чтобы эффективно запретить маршрут между ними.
Таблица расстояний.
Воспользуемся Таблицей расстояний из задачи для трех мусоровозов и 28 точек посещений.
Напомню, что мы моделировали координаты 27 точек посещения датчиком случайных чисел и вычисляли расстояния между этими точками посещения по известной математической формуле.
Получим примерно такую Таблицу расстояний:
Таблица расстояний для задачи с двумя машинами и 27 точками посещения На карте точки посещения выглядят так: Торговые точки и центральный склад на карте
Таблица переменных.
Подготовим таблицу переменных, добавив слева стандартной таблицы запросы каждой торговой точки.
При этом будем считать, что точки n01, n02 и n03 потребности в товаре не имеют.
Запрос в товаре определяет необходимое число машин. В чем измеряется запрос каждой торговой точки нам неважно, пусть это будут картонные короба с товаром. Общее количество коробов, которые нужно развести по торговым точкам - 1777, а вместимость машин 950. Следовательно, для развоза товара достаточно будет двух машин.
Для решения с двумя машинами выключим посещение точки n03 из маршрута.

Таблица переменных для решения задачи Построения маршрута двух мусоровозов.
Таблица специальных ограничений.
Макет таблицы специальных ограничений с новыми переменными
Установки OpenSolver.
Все подготовленно для решения задачи. Для поиска оптимального маршрута используем OpenSolver Oграничения на панели OpenSolver-Model при решении задачи для двух машин с учетом их вместимости
Решение, найденное OpenSolver.
При оптимизации можно использовать и Gurobi, и CBC, но решение с последним может занять полчаса или больше. В результате получим маршрут, общая длина которого 95,54 км. Маршрут для двух машин из 28 точек забора мусора, учитывающий вместимость машин
Таким образом, первая машина посещает 19 точек и развозит 936 коробов, а вторая машина посещает 10 точек и развозит 841 короб.

2

Решение задачи для трех машин с учетом их вместимости.

К сожалению, получение планов для трёх и более машин приходится добывать экстенсивным методом: каждая новая машина требует дополнительного набора переменных, аналогичных уже введенным.
Предположим, что вместимость машины - 750 коробов, а не 950, как мы рассматривали выше. Тогда для развоза товара необходимо задействовать 3 машины.
Что нужно изменить в уже созданных таблицах.
Таблицу расстояний менять не нужно, а в таблице переменных необходимо включить точку n03. Таблица переменных для решения задачи трех мусоровозов с учетом их вместимости.
В таблицу специальных ограничений нужно ввести две дополнительные переменные.
Будем искать точки посещения для 1 и 3 маршрута, а точки посещения 2 маршрута найдем как разность между всеми точками и точками 1 и 3 маршрута.
Макет таблицы специальных ограничений с двумя новыми переменными
Что нужно изменить в установках OpenSolver.
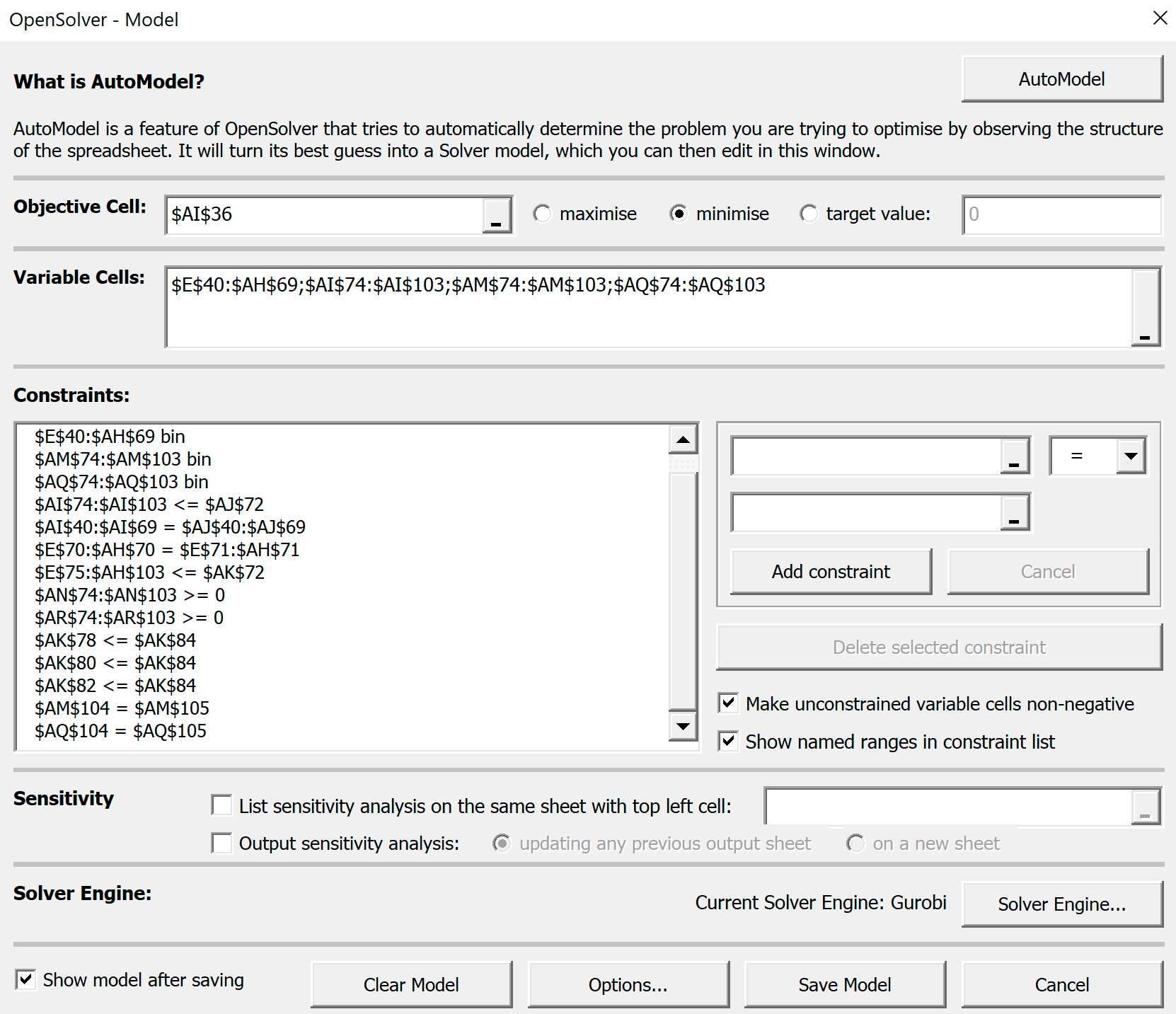
Oграничения на панели OpenSolver-Model при решении задачи для двух машин с учетом их вместимости Маршруты трех машин при учете вместимости
Теперь не меняя ничего в установках OpenSolver, можно исследовать построенную модель, например, изменив максимальную вместимость машины.
Маршруты трех машин при максимальной вместимости 675 коробов
Скачать файл с задачей Скачать файл "garbage_truck_route 6m.xlsx" (примерно 383 Кб)
Далее, чтобы использовать рассмотренную нами модель решения задачи нужно автоматизировать создание новых переменных програмным путем, либо разбивать задачу на подзадачи. Последний вариант ухудшит красоту решения, поскольку мы в модели все время искали единый оптимальный маршрут.
✉ Если у вас появились вопросы или замечания, вы можете предложить лучшее решение, то пишите мне на электронную почту.