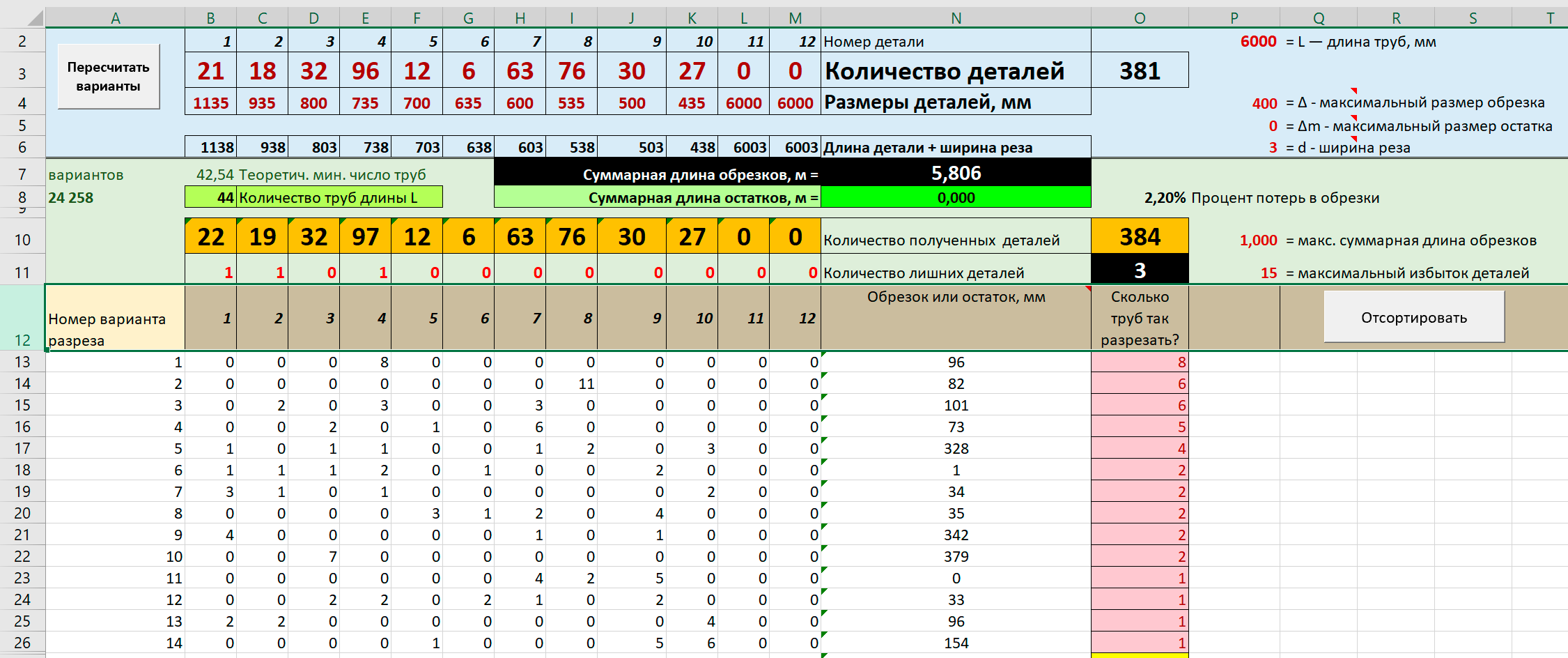
- Алгоритм решения всех задач о нарезке - длинномерных объектов или выкроек из листов - содержит два этапа:
- Перечисление всех возможных вариантов нарезки.
- Выбор наиболее удобных вариантов, удовлетворяющих дополнительным условиям.
Какие это могут быть условия?
К чему нужно стремиться?
Должно быть минимальное количество неиспользуемых обрезков!
Не изготавливать никаких лишних деталей!
Какое количество лишних деталий допустимо изготовить?
Какие минимальные остатки материала допустимы?
1
Расчет возможных вариантов нарезки трубы.
Фактически перечисление всех допустимых вариантов нарезки можно выполнить только программным путем. Так что вначале требуется написать программу (например, макрос VBA), фиксирующую все возможные варианты.
Для случая произвольных вариантов разрезания одной трубы на различные патрубки написать универсальную программу с неограниченным
числом задаваемых размеров деталей довольно сложно. Чтобы упростить дело, приходится исходить из заранее заданного
максимального количества типоразмеров.
В программе, которая разбирается далее, максимальное количество типоразмеров равно 12.
В программе, которая разбирается далее, максимальное количество типоразмеров равно 12.
- Допущения, параметры и их обозначения, используемые в программе:
L - длина трубы (в мм), из которой нарезаются патрубки;-
Номер детали - максимальное количество размеров деталей в заказе 12; -
Размеры деталей - задаем набор размеров деталей в мм; -
Количество деталей - количество деталей заданного размера;
Допущение: если набор деталей меньше, чем 12, то в лишние позиции записываем нулевые количества и размер равный длине трубы. d - ширина реза - ширина разреза отрезного диска в мм;Δ - максимальная длина обрезка в мм (максимальный размер неиспользуемых в дальнейшем обрезков, всё, что потом идет в металлолом);Δm - максимальный размер остатков трубы, который допустимо планировать, в мм;
Допущение: Остаток трубы – это обрезок длиной отΔ доΔm , который возможно использовать в дальнейшем. Нужно отметить, что если разрешить остатки длиной, скажем, 5 метров (5000 мм), то макрос предпочтет отрезать от труб по одному патрубку, чтобы так избежать возникновения неиспользуемых обрезков.
- Все эти данные вводятся в голубой блок программы и выглядят так:
- черным цветом выделены ячейки, в которых записаны формулы или комментарии. Значения в этих ячейках менять не нужно;
- красным цветом выделены ячейки, значения которых можно менять взависимости от условия конкретной задачи.
Нажатие на кнопку "Пересчитать варианты" запускает макрос VBA, который в нижней части листа от строки 13 создает список всех возможных разрезов.
Из всех мыслимых вариантов отобраны только варианты с обрезком короче заданной величины Δ или остатком от Δ до Δm.
Таким образом, варианты отреза от трубы длиной 6 м метровой детали с остатком 5 м в данном решении исключены.
В показанном варианте решения набор ограничен 10 видами деталей. Суммарное число вариантов всегда велико и зависит и от минимального допустимого обрезка, и от длины остатка, и от набора деталей.
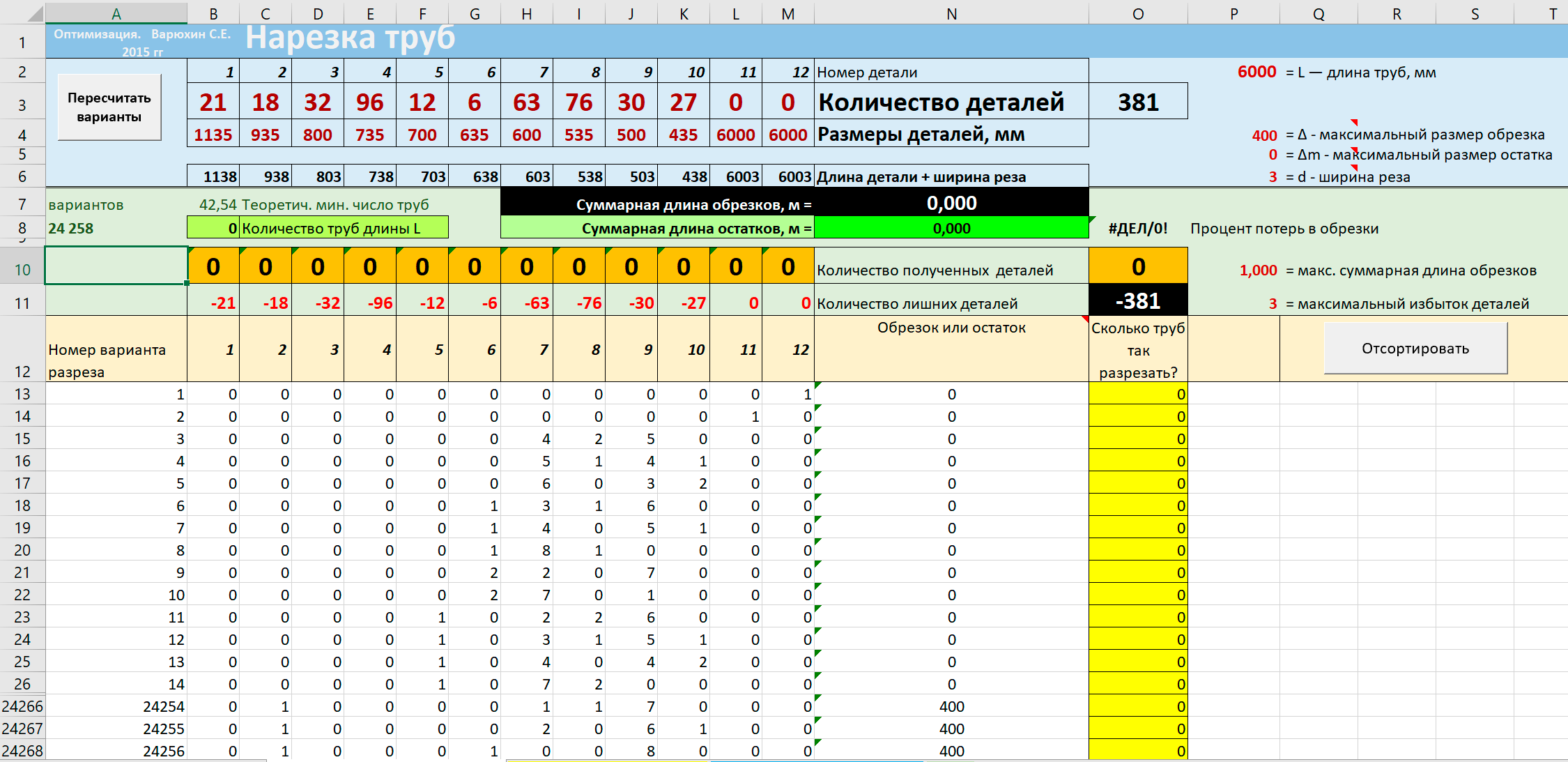 В данном случае число вариантов достигает 24 258.
В данном случае число вариантов достигает 24 258.
Этот файл будет работать на вашем компьюторе только, если установлен OpenSolver.
Штатный Поиск решения НЕ может решить задачу содержащую более 200 переменных. В этой задаче их десятки тысяч!
Рассотрим блок в зеленых тонах нашего файла. Это блок показывает результаты вычислений.2
Как выбрать лучшие варианты нарезки труб.
Выбор нужных вариантов нарезки труб делается из всех полученных вариантов. При этом решается задача целочисленной линейной оптимизации, из всех возможных вариантов вибираются лучшие. А переменные показают, сколько труб нужно нарезать каждым из выбранных вариантов.Переменные задачи - это ячейки столбца Сколько труб так разрезать?. В программе они выделены желтым цветом.
При нажатии клавиши Пересчитать варианты запускается макрос, который вычисляет различные варианты нарезки, находит суммарное число вариантов, корректирует расчетные формулы и установки оптимизатора. Для выбора наилучших вариантов нужно просто запустить Solver, предварительно проверив в модели наличие требуемых ограничений.
Для этого:
В меню MS Excel выберите вкладку Данные и нажмите Model
У вас появится панель OpenSolver - Model, в которой нужно проверить уже установленные макросом ограничения и при необходимости скорректировать любое ограничение или добавить новое.
Задача: Минимум обрезков
Рассмотрим решение этой задачи при условии, что мы хотим нарезать трубы так, чтобы обрезков было минимальное количество.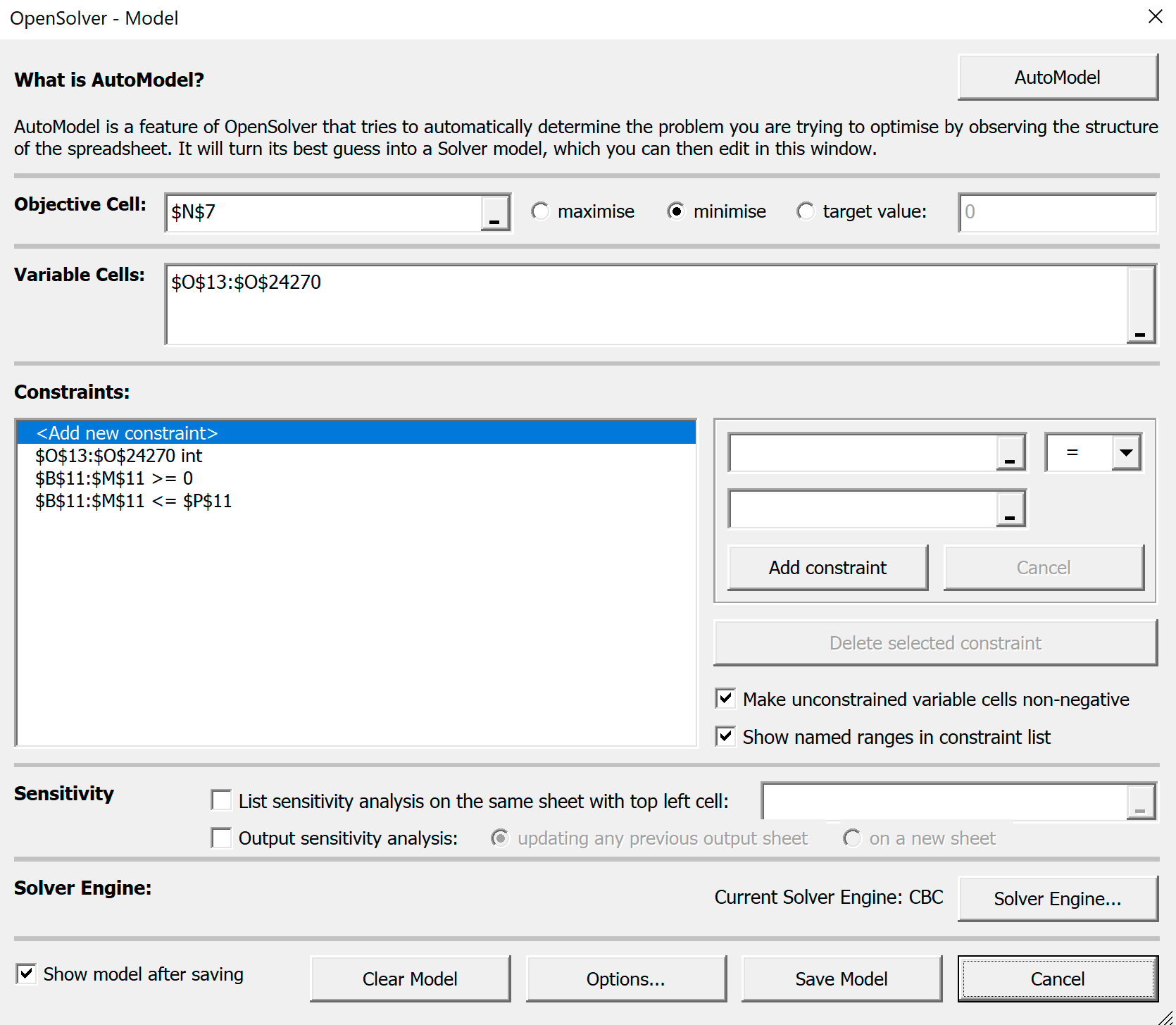
В установках OpenSolver целевая ячейка N7 - суммарная длина бросовых обрезков. Это значение должно быть минимальным.
Переменные ячейки$O$13:$O$24270 – сколько труб разрезать данным способом (24 258 переменных).
Сохраним модель и запустим решение. Для этого сначала нужно нажать Save Model на панели OpenSolver - Model, а затем клавишу SolveПеременные ячейки
- Введенные ограничения:
- Число разрезаемых труб должно быть целым.
Это ограничение реализует строка$O$13:$O$24270 int - Должно быть нарезано не меньше планового количества деталей.
Это ограничение реализует строка$B$11:$M$11>=0 - Количество произведенных лишних деталий заданного размера должно быть не больше заданного числа.
Это число устанавливается в ячейке
P11 . Это ограничение реализует строка$B$11:$M$11 <= $P$11
OpenSolver решает данную задачу около минуты, причем почти все время уходит на анализ параметров и построение задачи в памяти компьютера.
Характерные нормальные времена собственно оптимизации составляют в этой задаче от нескольких секунд до 5 минут (текущее время расчета можно увидеть в полосе состояния справа).
Если же задача продолжает считаться дольше, скорее всего ждать не имеет смысла – счет может продолжаться много часов. Остановить счет можно нажатием кнопки Esc.
Вполне может быть, что решение и будет найдено за 10 часов. Или за сутки. Но какой в этом практический смысл? Лучше попробовать изменить ограничения.
Рассмотрим полученное решение. Нажмите клавишу Отсортировать, чтобы найденные результаты выводились
вначале списка. Эти ячейки выделены розовым. Если же задача продолжает считаться дольше, скорее всего ждать не имеет смысла – счет может продолжаться много часов. Остановить счет можно нажатием кнопки Esc.
Вполне может быть, что решение и будет найдено за 10 часов. Или за сутки. Но какой в этом практический смысл? Лучше попробовать изменить ограничения.

Убрав ограничение о максимальном избытке деталей конкретного размера, мы получили решение, в котором нужно разрезать 212 труб ( вместо теоретических 43 ) и получить 2311 лишних деталей при заказе 381. Это явно за пределами разумного! Хотя обрезков при этом вообще не получается и целевая ячейка N7 равна 0.
В оптимальном решении, полученном только при требовании, чтобы деталей было не меньше заданного количества,
лишних деталей получается много!
Очевидно, что возможность нарезать лишние детали нужно как-то ограничить.
При этом требование, ограничивающее количество лишних деталей (либо каждого вида, либо суммарное), не является заведомо выполнимым.
Вполне может быть, что возможно найти решение вообще без лишних деталей, но заранее это неизвестно. Может быть, такого решения нет вообще. Приходится экспериментировать.
Введем снова ограничение При этом требование, ограничивающее количество лишних деталей (либо каждого вида, либо суммарное), не является заведомо выполнимым.
Вполне может быть, что возможно найти решение вообще без лишних деталей, но заранее это неизвестно. Может быть, такого решения нет вообще. Приходится экспериментировать.
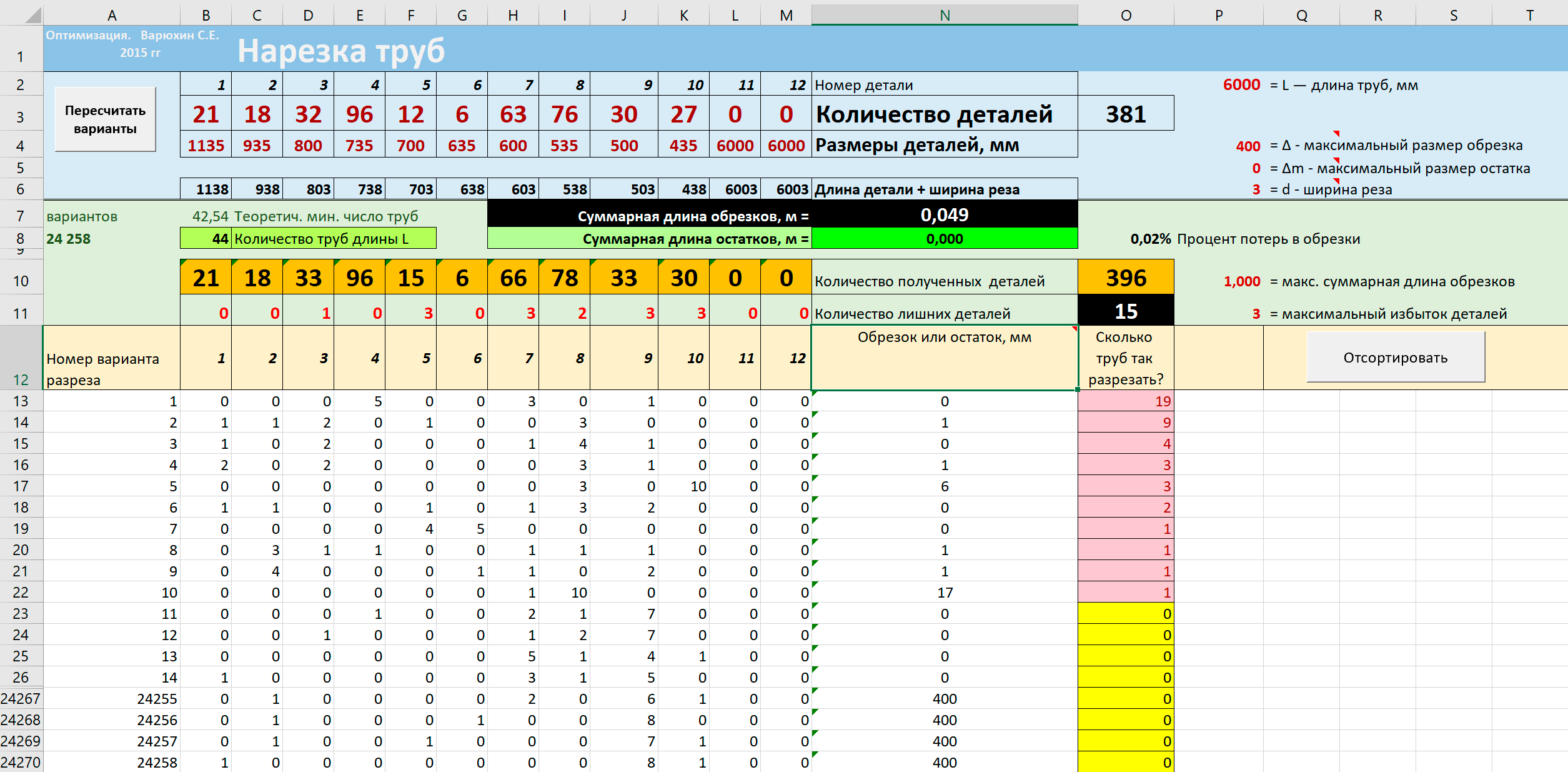
Мы получили довольно хорошее решение, в котором предлагается выполнить заказ, нарезав 44 трубы 10 разными способами. При этом получится избыток всего 15 деталей и обрезков 5 см. Если посмотреть, на решение, то видно, что эти 5 см складываются из обрезков от 1 до 17 мм, что реально приближает решение к искомому 0.
Задача: требуем минимальное количество лишних деталей.
Можно ограничивать и суммарное число лишних деталей. Для этого ограничение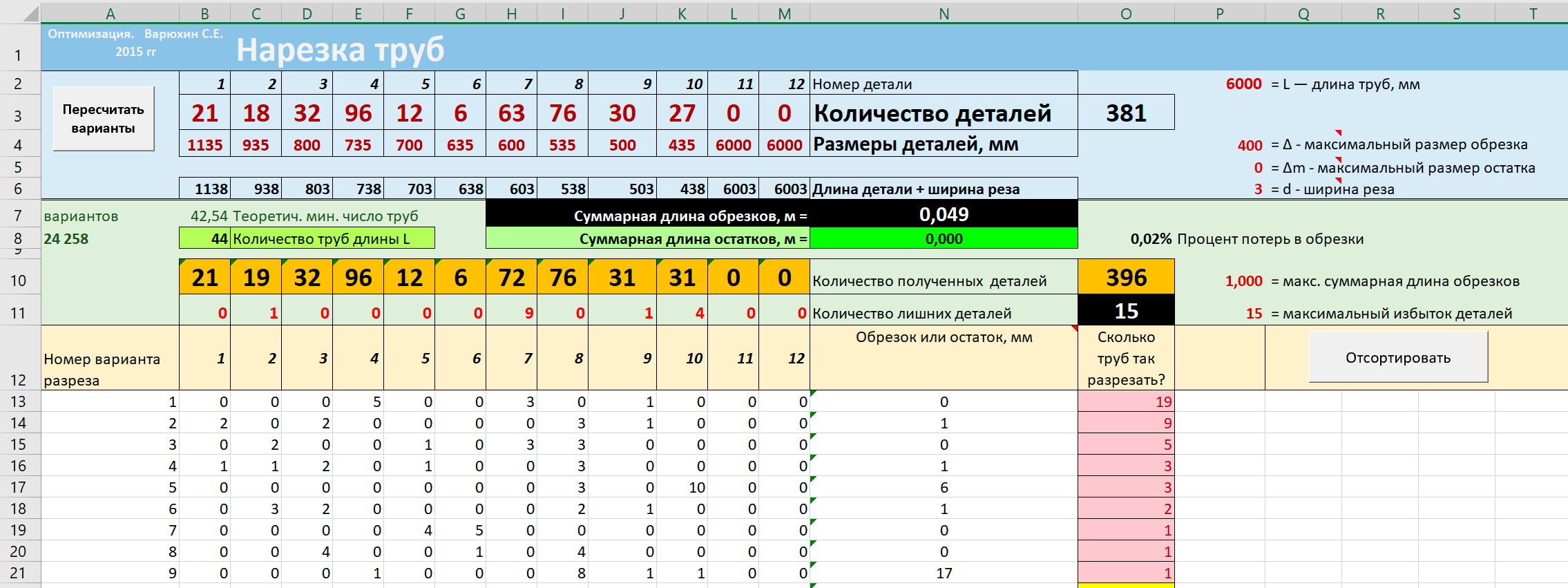
Теперь программа предлагает 9 вариантов раскроя труб. Но попытка еще уменьшить избыток деталей приводит к резкому росту времени расчета и решение даже для избытка в 14 деталей занимает неопределенно большое время.
Неизвестно, можно ли использовать лишние детали, но из самых общих соображений скорее всего имело бы смысл уменьшить их число, насколько возможно, допустив некоторое количество обрезков.
Чтобы получать решения с наименьшим количеством лишних деталей имеет смысл заменить целевую функцию
В этом случае ограничения на суммарное количество лишних деталей можно убрать.

Получили решение, при котором число деталей хоть и уменьшилось, но зато появились 6,8 метров обрезков. Это нуждается в разъяснении.

Если решение обычных задач линейной оптимизации не требует дополнительного исследования - оптимальное ли решение получено, то с целочисленной оптимизацией ситуация совершенно иная.
Лежащий в ее основе механизм оптимизации, вообще говоря, требует дополнительных настроек параметров алгоритма.
При решении небольших задач в это не обязательно вникать, оптимизация аккуратно проходит при установках параметров по умолчанию.
Однако при решении задач с большим количеством целочисленных переменных достигнутая глубина оптимума может сильно зависеть от выставленных установок параметра допустимого отклонения (Branch and Bound Tolerance, см. Model/Options).
Однако при решении задач с большим количеством целочисленных переменных достигнутая глубина оптимума может сильно зависеть от выставленных установок параметра допустимого отклонения (Branch and Bound Tolerance, см. Model/Options).

Параметр tolerance по умолчанию задают обычно равным 5%, так как уменьшение его приводит не только к росту точности поиска оптимума, но и к сильному росту времени поиска.
С практической же точки зрения разница в целевой функции между оптимумом найденным с tolerance=5% за несколько секунд и оптимумом с tolerance=0,1%, найденным за полчаса-час, может оказаться несущественной. Во всяком случае, когда мы говорим о задачах реального бизнеса, а не о чистой математике.
Зададим его равным 1%. При этом получим результат:
А при значении 0,1% находится решение, в котором вообще нет лишних деталей.

Правда, суммарная длина обрезков получается более 8 метров, но в процентах от длины использованных труб (44 труб всего, ячейка B8) это 3,26%. Чисто умозрительно – не так уж мало, но лучше бы сравнить это с долей потерь при текущем методе планирования.
Задача: Ограничиваем суммарную длину обрезков.
Предположим, что мы хотим, чтобы максимальная суммарная длина обрезков должна быть меньше 1 м. Добавим ограничение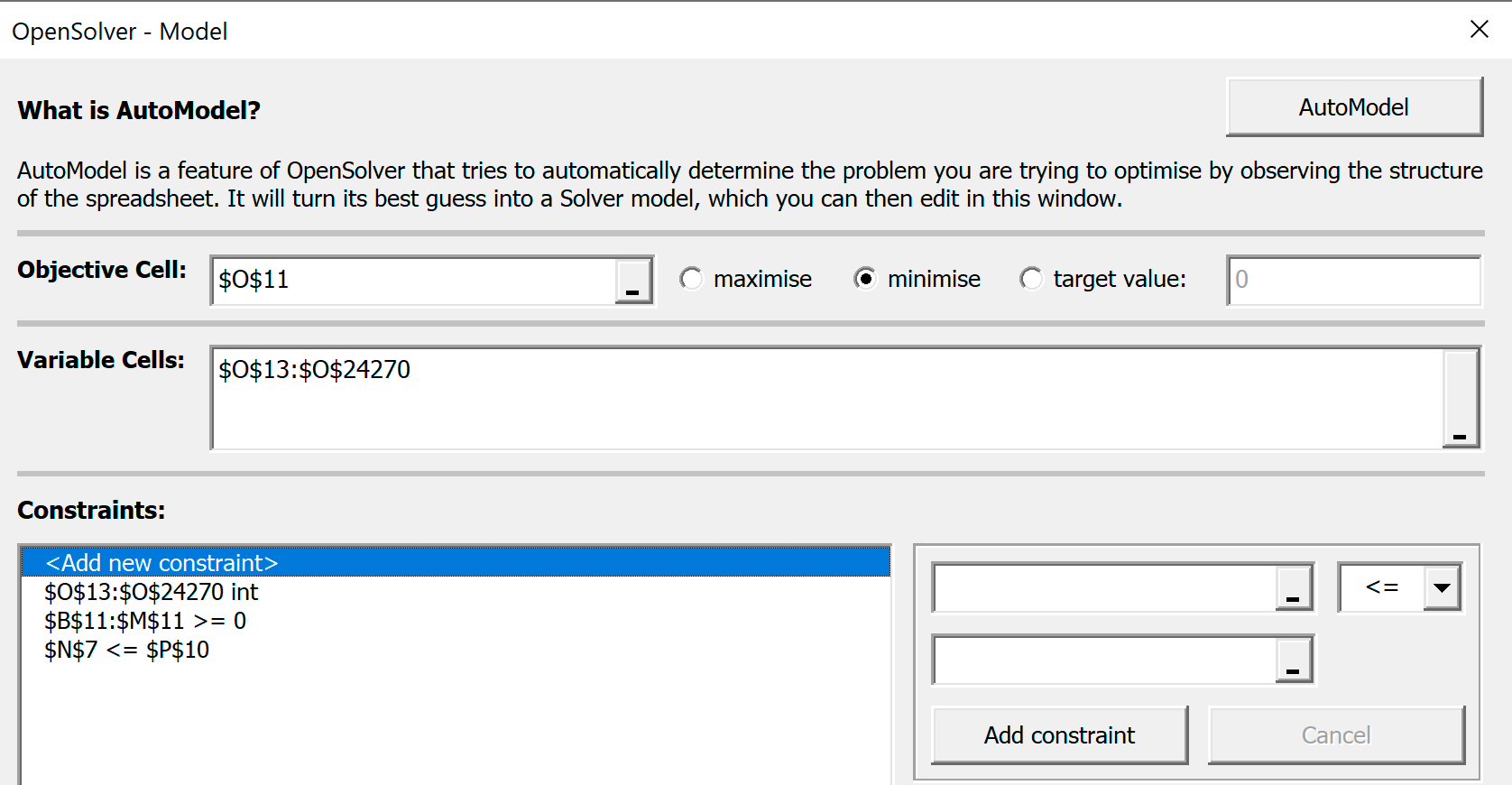
Получим резкое улучшение по обрезкам и три добавочные детали.

Процент потерь падает до 0,38%, число раскраиваемых труб до 43 (ячейка
В данном случае, даже если выбросить в металлолом лишние 3 детали, все равно отходы окажутся меньше 2,65 метров, т.е. 1%.
Очень неплохое решение!
Вы видите, что с решениями можно экспериментировать и дальше.
Желательно только уточнить, что же выгоднее всего…
Желательно только уточнить, что же выгоднее всего…
✉ Если у вас появились вопросы или замечания, вы можете предложить лучшее решение, то пишите мне на электронную почту.
 Скачать файл "Задача о нарезке труб" (примерно 8 Мб)
Скачать файл "Задача о нарезке труб" (примерно 8 Мб)