Кейс: Рулетка.

Предположим, что вы имеете возможность вложить 40 000€ в некий проект.
После определенного времени вы можете получить назад до 100 000€. К сожалению, эта инвестиция высоко-рисковая, так что на самом деле назад вы с равной вероятностью может получить любую сумму от 0 до 100 000.

1. Какова ваша средняя ожидаемая прибыль?
2. Какова вероятность потерять деньги? Потерять более 20 тыс.? Потерять все?
3. Какова вероятность получить не менее 50 тыс. прибыли? Получить от 8 до 16 тыс. прибыли?

1

Моделируем задачу.

Таким образом, для моделирования задачи нам необходимы три величины:
• значение рулетки - случайное число, которое иммитирует рулетку и определяет, какой доход мы получим.
• доход, который мы можем получить. Так как случайное число генерируется в интервале от 0 до 1, а по условию задачи мы можем получить назад от 0 до 100 тысяч, то
  доход (в тысячях евро) = значение рулетки * 100
• прибыль - это финансовый результат, который мы получим в результате этой инвестиции
  прибыль (в тысячах евро) = доход - 40

Модель задачи

Как определить вероятность получить тот или иной выигрыш и найти среднюю ожидаемую прибыль?

2

Расчитываем вероятностные характеристики.

Для этого:
• перенесем модель на рабочий лист MS Excel;
• откроем надстройку Моделирование Монте-Карло;
• в качестве целевых ячеек укажем ячейки, в которых вычисляется доход и прибыль.
• Запустим надстройку.

Итак,
• Средний ожидаемый доход - 50 ± 0,6 тысяч
• Средняя ожидаемая прибыль - 10 ± 0,6 тысяч
У вас при моделировании возможно будут чуть другие цифры, но, так или иначе, близкие к 50 и 10.

Откроем лист с гистограммами:
• Гистограмма дохода.
    Мы разбили горизонтальную ось на 20 интервалов по 5 единиц. Сама горизонтальная шкала соответствует возможному доходу от 0 до 100. Мы видим более менее равномерное распределение попадания случайной величины в указанные интервалы. Тем не менее отдельные столбцы отличаются по высоте, хотя ширина интервалов, на которые мы разбиваем шкалу от 0 до 100 одинакова.
  В колонку 5 попадают все выпавшие значения от 0 до 5 включительно, в следующую все значения больше 5 но меньше или равно 10 и т.д.
  Понятно, что если распределение равномерное, то в каждый интервал должно упасть одинаковое количество результатов. Проводя 10 тысяч испытаний мы ожидаем, что в каждую колонку должно упасть примерно 500 результатов (10 тысяч/20 = 500). Но поскольку мы имеем дело со случайной величиной, то в каждый столбец падает немного разное количество результатов. В какие-то интервалы попадает больше 500, а в какие-то меньше. Тем не менее, мы видим, что вероятность случайной величины попасть в любой отдельно взятый столбец близка к 5% (500/10000 = 0,05 = 5%).
• Гистограмма прибыли.
  В колонку -35 попадают все значения от -40 до -35 включительно, в следующую все значения больше -35 но меньше или равно -30 и т.д.
Таким образом,
• вероятность получить доход в диапазоне от 0 до 5 тысяч близка к 5% ;
• вероятность получить доход в диапазоне от 10 до 15 тысяч тоже близка к 5%, но вероятность получить доход не ниже 10 тысяч уже примерно 10%, так как к этому варианту относятся уже 2 столбца: получить доход от 0 до 5 и получить доход от 5 до 10. Вероятность каждого события 5%, поэтому суммарная вероятность - 10%.;
• вероятность получить доход не больше 40 тысяч равна примерно 40% (складываем вероятности столбиков гистограммы. Так как столбиков 8, то 8*5%=40%);
Аналогично с прибылью.
• Вероятность потерять деньги в диапазоне от 40 до 35 тысяч близка к 5%.
• Вероятность потерять деньги в диапазоне от 35 до 30 тысяч тоже близка к 5%, а вероятность потерять деньги от 40 до 30 тысяч уже примерно 10%.
• Вероятность потерять 20 тысяч складывается из суммы вероятностей попасть в столбцы левее 20 тысяч на гистограмме, а также в этот столбец. Таких столбцов 4, поэтому вероятность потерять 20 тысяч евро составляет 20% (5% * 4 = 20%).
• Вероятность потерять деньги от 40 тысяч до 0 примерно 40% .
• Вероятность получить прибыль 5 тысяч - 5%, а вероятность получить прибыль от -40 тысяч до 10 тысяч почти 50%.
  Поэтому на вопрос: какова вероятность заработать не более 10 тысяч? Ответ: эта вероятность равна 50%.
• Вероятность получить прибыль выше 50 тысяч, это вероятность попасть в два последних столбца, и она составляет примерно 10%.
Мы научились читать гистограммы и находить по ним вероятности наступления определенного события.


А если увеличить число испытаний до 100 тысяч, что изменится?

В соответствии с теорией, при увеличении статистики наша оценка среднего значения случайной величины должна стать точнее, так как колебания случайной величины относительно среднего значения должны стать меньше.
• Как видим, при 100 тысячах испытаний колебания высоты столбиков гистограммы стали меньше. Поэтому наша оценка вероятности попадания случайной величины в тот или иной диапазон от 0 до 100 стала точнее, и все больше приближается к 5%.
• Тоже можно сказать и для гистограммы прибыли.

3

Изменим условие задачи.

Предположим, что у нас есть возможность вложить деньги в два независимых проекта. В каждый проект вложим 20 тысяч евро. Теперь от каждой инвестиции мы можем получить от 0 до 50 тысяч евро.

Какова вероятность потерять инвестиции в этом случае?

Какова вероятность получить больше 50 тысяч прибыли в этом случае?



Снова построим модель задачи.
• Теперь нам необходимо генерировать два случайных числа, каждое из которых моделирует степень успеха отдельного проекта.
• Доход вычисляем как сумму дохода от каждого проекта:
  доход = 1 случайное число * 50 + 2 случайное число * 50
• Прибыль - это разность между совокупным доходом и инвестицией:
  прибыль = доход - 40

Модель задачи

Значение рулетки:
Значение рулетки:
Доход:
Прибыль:
Твой шанс
Результаты игры:

1 проект	вложено 20 тыс.	2 проект	вложено 20 тыс.
Доход	Прибыль	Доход	Прибыль


Проведя ряд испытаний, мы видим, что финансовые результаты проектов не зависят друг от друга, и мы попрежнему можем либо потерять деньги, либо что-то заработать. Расчитаем вероятностные характеристики этой задачи.
Для проведения большого числа испытаний снова обратимся к методу Монте-Карло.
Для этого:
• перенесем модель на рабочий лист MS Excel.
  Нам потребуются 4 ячейки на рабочем листе:
  • две ячейки, в которые мы введем функцию СЛЧИС()
  • ячейка для вычисления дохода
  • ячейка для вычисления прибыли
• откроем надстройку Моделирование Монте-Карло;
• в качестве целевых ячеек укажем ячейки, в которых вычисляется доход и прибыль.
• Запустим надстройку.
Получим новый результат:

Как видим,
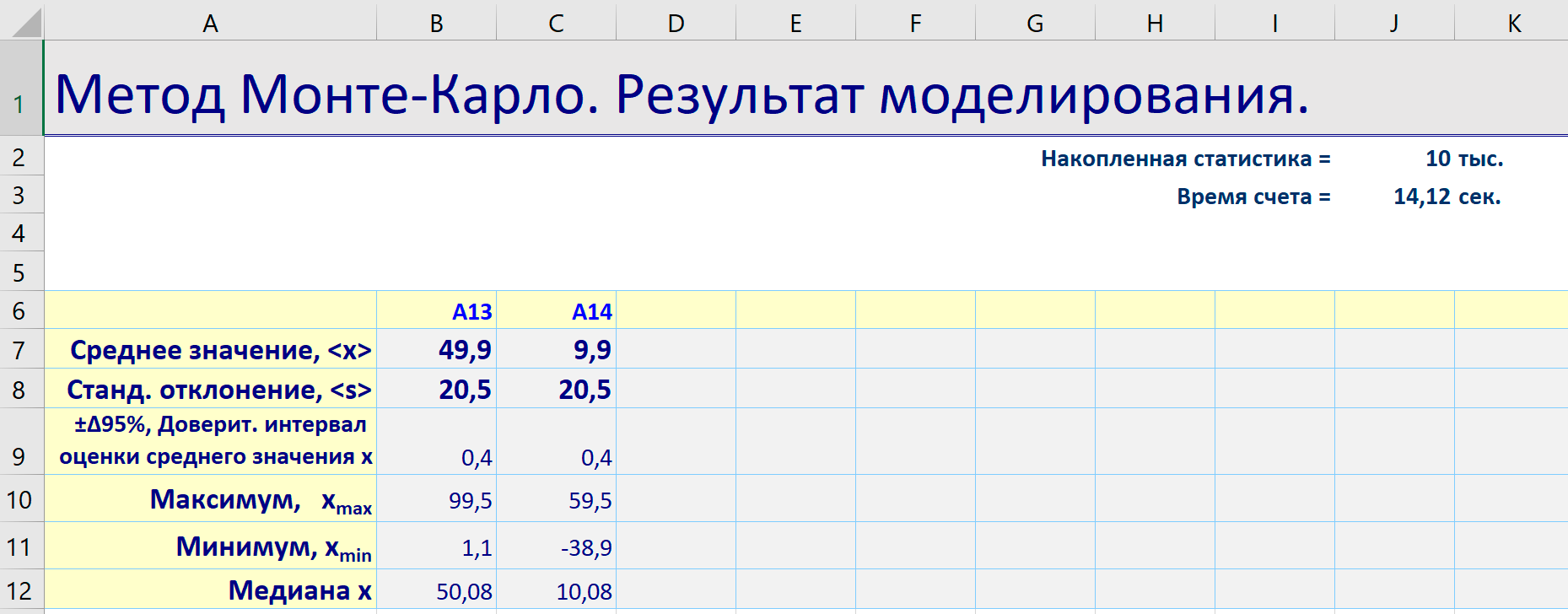
1. Суммарный средний ожидаемый доход от наших инвестиций по-прежнему близок к 50 тысячам - 49,9 ± 0,4.
2. Средняя ожидаемая прибыль также остается около 10 тысяч евро - 9,9 ± 0,4.
3. Уменьшилось значение стандартного отклонения. А это значит, что колебания вокруг средней величины для двух проектов меньше, чем для одного.
   
4. Уменьшилось значение доверительного интервала. А это значит, что выросла точность определения нашей случайной величины: среднего ожидаемого дохода и средней ожидаемой прибыли.
Но посмотрим теперь на гистограммы.
• Гистограмма дохода:
• Гистограмма прибыли:
На обоих гистограммах вместо равновероятностного распределения мы видим ярко выраженные треугольные формы, а это значит что результаты отдельных опытов стремятся к среднему значению.
Как это объяснить?
Почему гистограммы распределения дохода или прибыли имеют треугольную форму?
Рассуждаем:
• В каком случае мы получим нулевой доход?
  • в том случае, когда вложения в оба независимых проектов будет неудачным и доходы от обоих проетов будут 0.
• В каком случае мы получим доход в 5 тысяч?
  здесь вариантов уже больше:
  • доход от 1 проекта - 0, доход от 2 проекта - 5 и наоборот;
  • доход от 1 проекта - 1, доход от 2 проекта - 4 и наоборот;
  • доход от 1 проекта - 2, доход от 2 проекта - 3 и наоборот;
• В каком случае мы получим доход в 10 тысяч?
  здесь вариантов значительно больше:
  • доход от 1 проекта - 0, доход от 2 проекта - 10 и наоборот;
  • доход от 1 проекта - 1, доход от 2 проекта - 9 и наоборот;
  • доход от 1 проекта - 2, доход от 2 проекта - 8 и наоборот;
  • доход от 1 проекта - 3, доход от 2 проекта - 7 и наоборот;
  • доход от 1 проекта - 4, доход от 2 проекта - 6 и наоборот;
  • доход от 1 проекта - 5, доход от 2 проекта - 5;
• В каком случае мы получим доход в 100 тысяч?
  • только в том случае, когда оба проекта будут супер успешны и каждый из них принесет доход по 50 тысяч.
    А вероятность этого маленькая.

Как высислить вероятности, когда распределение случайной величины не является равномерным?


Конечно, можно продолжать складывать значения каждого столбца, но это очень неудобно.
Поэтому статистики придумали кумуляты.
Кумулята - это сумма с нарастающим итогом для первого столбца, для двух столбцов, для трех, четырех и т.д. до суммы всех столбцов.
Если вы перед запуском надстройки Моделирование Монте-Карло отметили флажком поле Кумуляты, то на третьем листе появившегося отчета вы найдете такие кумуляты.
• Кумулята дохода:
  • по горизонтальной оси отложены возможные значения дохода от 0 до 100.
  • по вертикальной оси отложены суммы вероятностей от 0% до 100%.
  
• Кумулята прибыли:
  • по горизонтальной оси отложены возможные значения прибыли от -40 до 60.
  • по вертикальной оси отложены суммы вероятностей от 0% до 100%.
  
По кумуляте легко ответить на интересующие нас вопросы: какова вероятность получить результат не лучше, чем заданное число?
• Так вероятность получить нулевую прибыль порядка 32%.
• Вероятность потерять больше 20 тысяч около 8%.
• Вероятность потерять все деньги 0,2%.
• Вероятность получить не менее 50 тысяч около 3% (100 - 97 = 3).
Что будет, если разложить инвестируемую сумму в два независимых проекта?
• средний ожидаемый доход и средняя ожидаемая прибыль не изменится.
• вероятность полной потери денег уменьшается с 5% до 0,2%.
• вероятность совсем не вернуть свои деньги (получить нулевую прибыль) уменьшается с 40% до 32%.
• вероятность получить большой выигрыш (получить больше 50 тысяч) падает с 10% до 3%.
Получив такой результат мы вправе задать вопрос:

А если положить 40 тысяч в 10 независимых проектов по 4 тысячи в каждый, то как изменится средний ожидаемый доход и средняя ожидаемая прибыль?

Исследуем этот вопрос.

4

Инвестируем в 10 независимых проектов.

У нас есть все те же 40 тысяч евро. Мы инвестируем в 10 независимых проектов по 4 тысячи евро. В результате мы можем получить доход от каждого проекта от 0 до 10 тысяч евро.
Построим модель этой задачи в рабочей книге MS Excel.
1. На рабочем листе MS Excel введем в 10 ячеек функцию СЛЧИС(). Значения в этих ячейках будут моделировать финансовые результаты независимых 10 проектов.
2. В ячейку для расчета дохода запишем формулу:
   1Случайное число * 10 + 2Случайное число * 10 + ... + 10Случайное число * 10.
   Очевидно, что формулу нужно упростить: Сумму всех десяти ячеек, в которые мы ввели функцию СЛЧИС() умножим на 10.
3. Прибыль считаем как и в двух предыдущих случаях:
   Доход - 40
4. Откроем надстройку Моделирование Монте-Карло, в качестве целевых ячеек укажем ячейки, в которых вычисляется доход и прибыль.
5. Запустим надстройку.
Получим новый результат.
Средний ожидаемый доход и средняя ожидаемая прибыль НЕ ИЗМЕНИЛИСЬ! Однако все остальные характеристики изменились довольно сильно:
• Средний ожидаемый доход 50,0 ± 0,2
• средняя ожидаемая прибыль 10,0 ± 0,2
• Максимальный размер дохода упал с 100 до 80; максимальное значение прибыли снизилось с 60 до 40.
• Минимальный размер дохода вырос с 0 до почти 16; минимальное значение прибыли выросло с -40 до -24.
А что произошло с гистограммами?
• Гистограмма дохода:
  • форма распределения вероятности ожидаемого дохода близка к нормальному распределению, а значит результаты отдельных опытов стремятся к среднему значению;
  • сузился интервал разброса ожидаемого дохода, теперь он стал от 20 до 80
  • вероятность получения среднего ожидаемого дохода увеличилась.
• Гистограмма прибыли:
  • форма распределения вероятности ожидаемой прибыли близка к нормальному распределению, а значит результаты отдельных опытов стремятся к среднему значению;
  • сузился интервал разброса ожидаемой прибыли, теперь он стал от -20 до 40
  • вероятность получения средней ожидаемой прибыли возрасла по сравнению с инвестициями в 2 проекта.
На обоих гистограммах распределение случайной величины приближается к нормальному распределению. Этот факт иллюстрирует справедливость Центральной предельной теоремы теории вероятности.


Центральная предельная теорема
Сумма большого числа примерно одинаковых случайных величин с произвольными функциями распределения всегда имеет распределение близкое к нормальному.

Обратим внимание на кумуляты и снова ответим на все интересующие нас вопросы:
• Кумулята дохода:
  
  • вероятности получить доход ниже 20 тысяч и выше 80 тысяч нулевые;
  • вероятности получить доход не ниже 40 тысяч - около 14%;
• Кумулята прибыли:
  
  • Вероятность потерять больше 20 тысяч - 0%.
  • Вероятность получить нулевую прибыль - около 14%.
  • Вероятность получить не менее 10 тысяч - 50%
  • Вероятность получить больше 40 тысяч прибыли - 0%
Итак, вложение денег в 10 проектов вместо одного мы
• НЕ УВЕЛИЧИЛИ ни средний ожидаемый доход, ни прибыль;
• УМЕНЬШИЛИ вероятность потерять много денег за счет уменьшения вероятности много выиграть.

5

Инвестируем в 100 независимых проекта

А если наши 40 тысяч евро инвестировать в 100 независимых проектов по 400 евро в каждый? Доход, который мы можем получить в результате отдельной инвестиции, теперь может быть от 0 до 1 тысячи евро. Как в этом случае изменятся наши вероятности?
Модель этой задачи в рабочей книге MS Excel по смыслу мало чем будет отличаться от предыдущего случая.
1. На рабочем листе MS Excel введем в 100 ячеек функцию СЛЧИС(). Значения в этих ячейках будут моделировать финансовые результаты независимых 100 проектов.
2. В ячейку для расчета дохода запишем формулу:
   1Случайное число * 1 + 2Случайное число * 1 + ... + 100Случайное число * 1.
   Очевидно, что формулу нужно упростить: Сумму всех десяти ячеек, в которые мы ввели функцию СЛЧИС() умножим на 1.
3. Прибыль считаем как и в двух предыдущих случаях:
   Доход - 40
4. Откроем надстройку Моделирование Монте-Карло, в качестве целевых ячеек укажем ячейки, в которых вычисляется доход и прибыль.
5. Запустим надстройку.
Получим новый результат.
Как и следовало ожидать
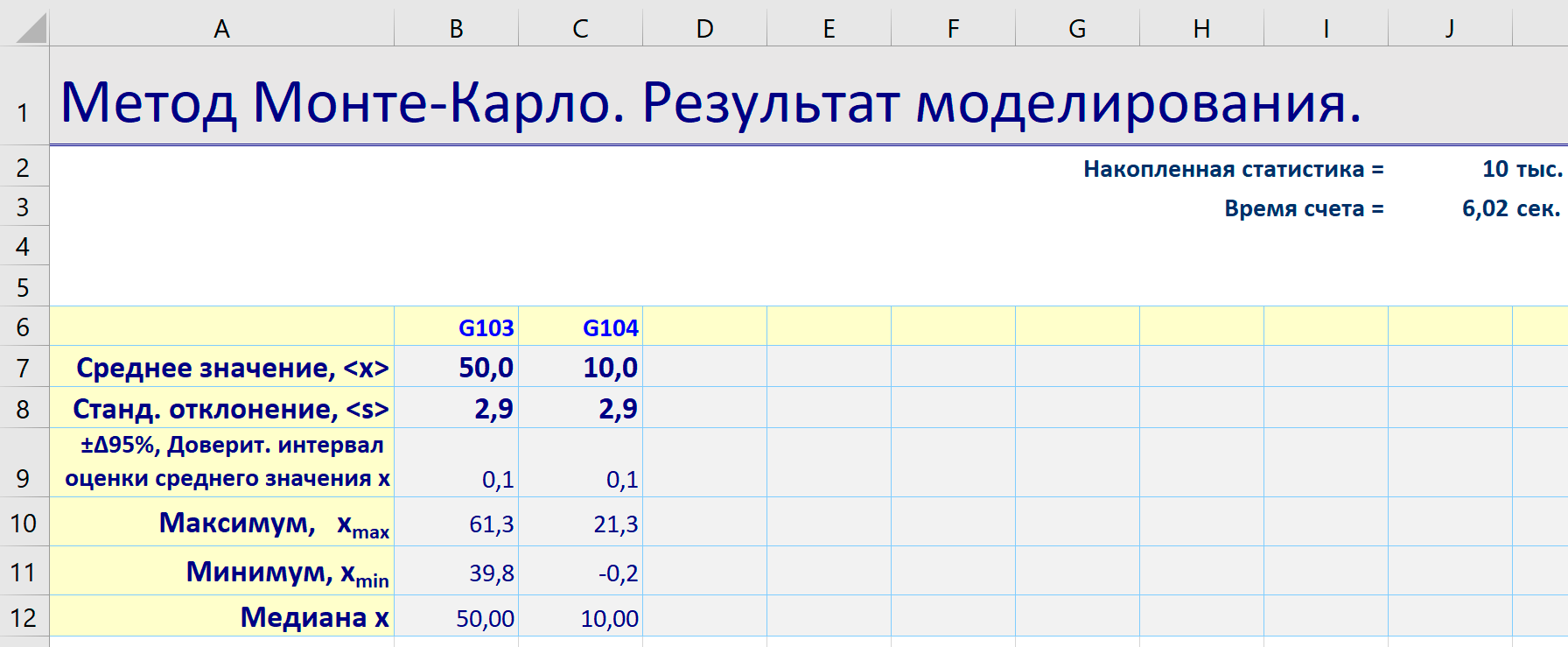
• Средний ожидаемый доход и средняя ожидаемая прибыль не изменились
• возрасла точность определения этих величин:
  • cредний ожидаемый доход - 50 ± 0,1
  • средняя ожидаемая прибыль - 10 ± 0,1
• уменьшился интервал вариации ожидаемого дохода. Теперь ожидаемый доход стал от ≈ 40 до ≈60
• соответственно уменьшился диапазон вариации ожидаемой прибыли от ≈ 0 до ≈20
А что произошло с гистограммами?
• Гистограмма дохода:
• Гистограмма прибыли:
• Выводы:
  • Распределение случайных величин стремится к нормальному
  • Сузился диапазон возможных значений случайной величины
  • Теперь мы фактически полностью исключили риск потери денег так же как и возможность получить больше выигрыши
• Кумулята дохода:
  
• Кумулята прибыли:
  
Для лучшего понимания наших выводов посмотрим на гистограммы дохода четырех вариантов вложения денег, сделанные в одном масштабе:
1 / 4

2 / 4

3 / 4

4 / 4

❮ ❯




Очевидно, что гистограммы ожидаемой прибыли, полученный в одном масштабе будут выглядеть похожим образом.
1 / 4

2 / 4

3 / 4

4 / 4

❮ ❯





6

Подводим итоги.

Совет игрокам в азартные игры:
Казино всегда имеет немного большую вероятность выиграть, чем вы. Так устроен этот бизнес. Эта вероятность чуть больше 50%.
Если вы хотите выиграть больше, то у вас есть только одна возможность: сделать ставку и смириться с результатом!
Если вы играете долго, то приближаетесь к среднему значению, и это значение не в вашу пользу. Вы приближаетесь к проигрышу.
Почему сеть устойчивее отдельно взятого розничного магазина?
• Если вместо одной торговой точки открыть 100 магазинов, то средний ожидаемый результат станет в 100 раз больше. И это очевидно, так как денег вложено в 100 раз больше.
• При этом, если магазины действительно независимы друг от друга, не отнимают покупателей друг у друга, находясь на соседней улице, то риски для сети существенно ниже, чем риск для одного магазина.
Почему не удается полностью диверсифицировать риски на рынке акций?
Ключевым условием полностью исключить риск потери денег является инвестирование в абсолютно независимые друг от друга компании.
Однако найти независимые друг от друга объекты невозможно, так как они все зависят от общей экономической коньюктуры. Поэтому полностью диверсифицировать риски невозможно. Но существенно уменьшить их получается, инвестируя средства в разные отрасти, в разные страны.