На самом деле разница между типичной «задачей навигатора» и «задачей коммивояжера» есть:
не все населенные пункты между заданными местами нужно посетить.
Эта разница приводит к колоссальному упрощению задачи.
Вместо сложной для вычислений «задачи коммивояжера» получается обычная «задача о назначениях» со всеми ее преимуществами!
не все населенные пункты между заданными местами нужно посетить.
Эта разница приводит к колоссальному упрощению задачи.
Вместо сложной для вычислений «задачи коммивояжера» получается обычная «задача о назначениях» со всеми ее преимуществами!
1
Организация данных для построения задачи. Таблица расстояний.
Чтобы не получилось излишне громоздко, не будем брать все населенные пункты из базы данных автомобильных дорог. Используем упрощенную схему.Для визуализации построенных маршрутов и расположения городов нам необходимы примерные координаты городов.
По этим координатам построим диаграмму расположения городов:
Теперь соберем все данные вместе и подготовим таблицу расстояний.
- Пояснения к таблице:
- Будем считать, что по вертикали перечислены города, из которых мы выезжаем, а по горизонтали – в которые въезжаем.
- Там, где прямой дороги нет, мы поставили 10000 для того, чтобы оптимизатор избегал эти участки при решении задачи оптимизации.
- Организауем данные в файле MS Excel.
- Перенесем данные о расстояниях по имеющимся участкам дороги в таблицу.
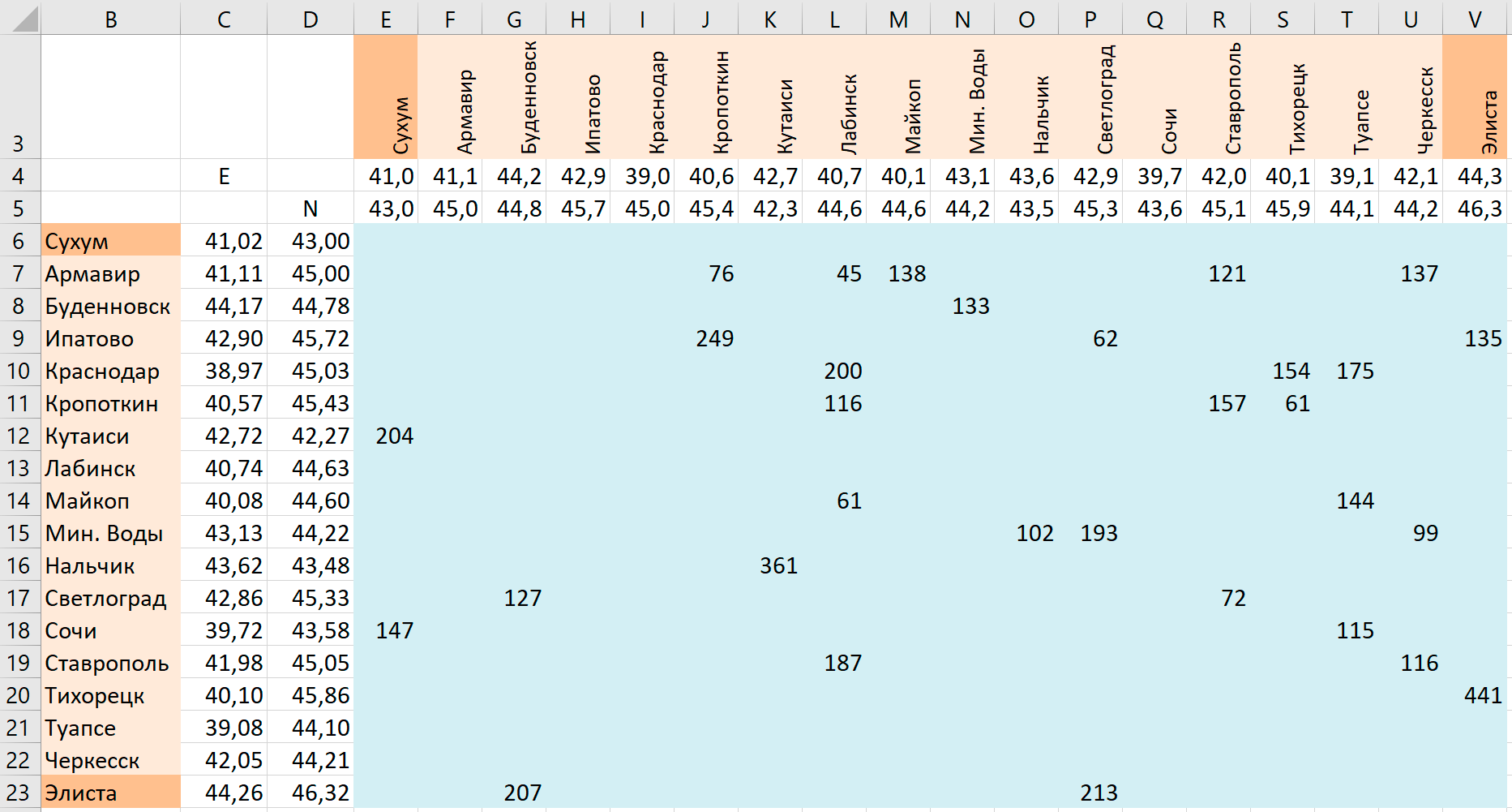
- Чтобы не думать о том, какое направление участка дороги нам нужно задавать, сделаем табличку симметричной относительно диагонали
Сухум\Сухум – Элиста\Элиста.
- Проще всего это сделать скопировав голубую область
E6:V23 и вставив ее временно в любое свободное место с транспонированием.
- Затем выделяем полученную копию, нажимаем CTRL+C, щелкаем ячейку
E6 правой кнопкой мыши, выбираем Специальная вставка и в появившейся панели отмечаем Операция – Сложить.
В этом случае при вставке скопированные ячейки складываются с имеющимися.

-
Так как в списке участков дороги ни один участок не дублируется
(нет вариантов
X-Y , а потомY-X ), то в изначальную таблицу просто добавятся все симметричные маршруты.
По строке информации Excel внизу нетрудно проверить, что в таблице был 31 участок дороги, а после вставки их стало 62.
Значит – все верно сделано, без ошибок.
В результате получится такая таблица:
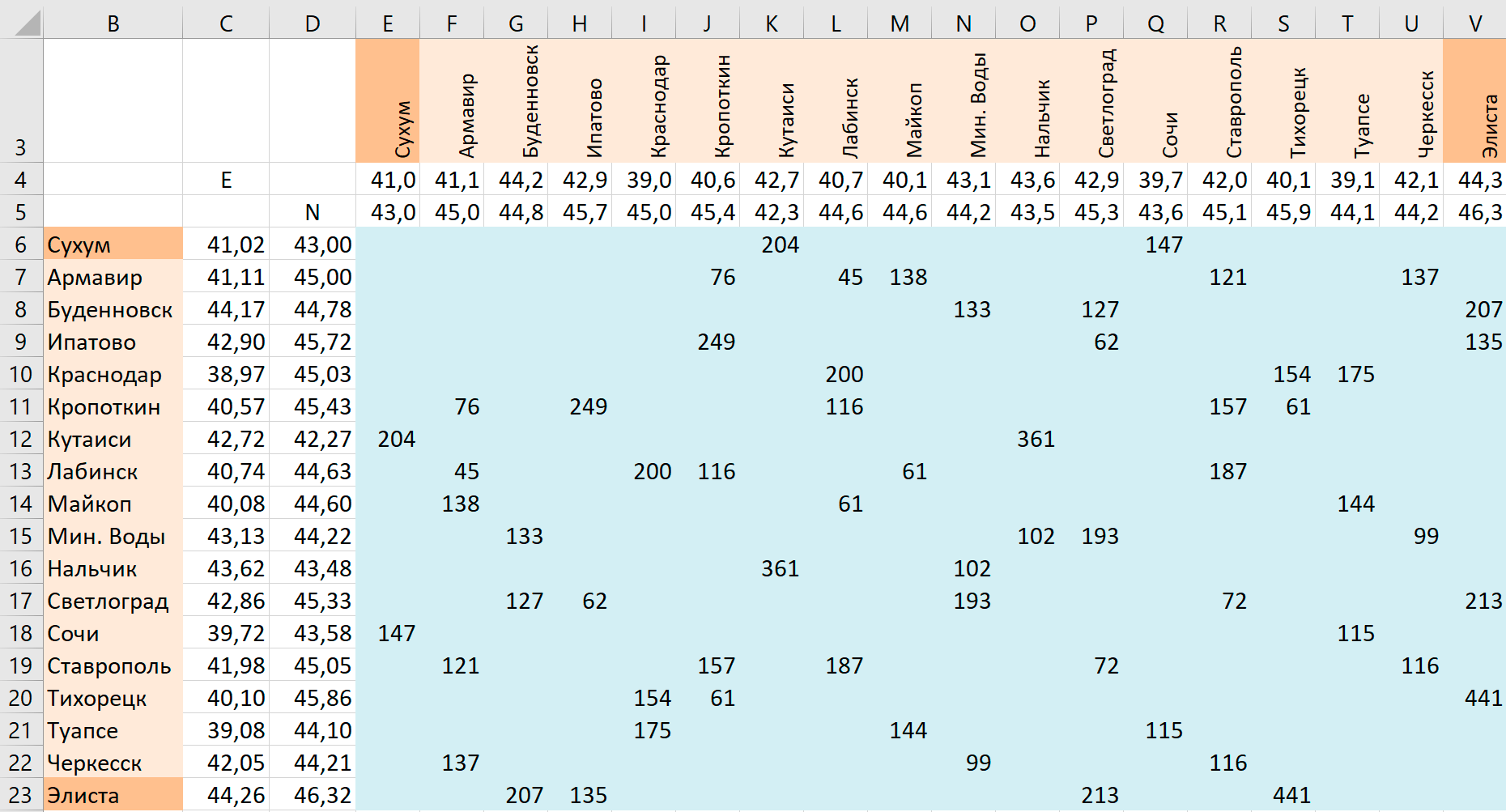
где длина участка не указана, прямой дороги нет . - Проще всего это сделать скопировав голубую область
- Формулы Excel обычно считают, что пустые ячейки содержат
0 . Поэтому, полученный вариант таблицы содержит множество разрешенных маршрутов с нулевой длиной. В том числе и участок Сухум-Элиста. Однако, в нашей задаче пустые ячейки - это участки, где нет дорог. Значит в задаче пустая ячейка - это запрещенный участок.
Чтобы не писать запретов в ограничениях удобно этим запрещенным участкам приписать аномально большую длину, чтобы при оптимизации алгоритм автоматически избегал включать их в полный маршрут, например, 10000 км.
Проще всего выделить еще раз голубую областьE6:V23 , выбрать команду Главная – Найти и выделить - Заменить. Появится панель, в которой в окне Найти пустое место, указать в Заменить на10000 .
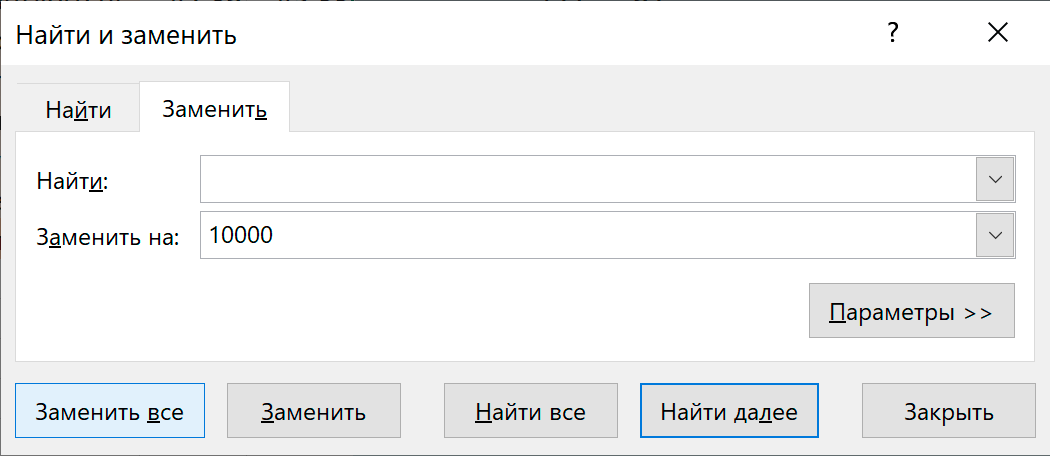
После этого сразу получим полностью заполненную таблицу расстояний

- В таблице намеренно ужата ширина столбцов, чтобы вместо чисел 10000 показывались знаки #.
Условное форматирование подкрашивает ячейки, содержащие 10000 так, чтобы выделить расстояния реально существующих участков дорог.
2
Таблица переменных для задачи "Маршрут навигатора".
Для решения задачи нам необходима Таблица переменных, которая должна соответствовать по размеру таблице расстояний.После решения задачи оптимизации в Таблице переменных цифрой
Отметим, что столбец
- Пояснения к таблице:
- Желтое поле - - это поле переменных. При решении задачи оптимизации в этих ячейках должны быть проставлены 1 (если участок попал в маршрут) и 0 (если участок не попал в маршрут).
- Оранжевые ячейки в желтом поле переменных должны всегда содержать 0.
- В каждую светло-коричневую ячейку 0введена формула, которая находит сумму желтых ячеек по соответствующей строке или соответствующему столбцу. Так как, пока значений в желтых ячеек нет, то все суммы равны
0 .
Смысл этой формулы: сосчитать, сколько раз каждый город назначен для выезда (суммы в столбце справой стороны таблицы) и сколько раз для въезда (суммы в строке внизу таблицы).
Потому что по смыслу прокладываемого маршрута для всех городов за исключением Сухума и Элисты число въездов в город должно быть равно числу выездов. Иначе мы застреваем в каком-то промежуточном городе. -
Коричневые ячейки 0дублируют значения светло-коричневого столбца. Эти ячейки мы будем использовать как ограничение в установках Open-Solver-Model.
Таблицу переменных удобно размещать под таблицей расстояний.
 Нам обязательно нужно сосчитать, сколько раз каждый город назначен для выезда (
Нам обязательно нужно сосчитать, сколько раз каждый город назначен для выезда (=СУММ(F28:V28) ) и сколько раз для въезда (=СУММ(F28:F45 )в ячейке F46 ).
Для контроля въездов-выездов запишем в ячейки строкиF47:U47 формулу =ТРАНСП(W29:W44) (напомним,
что это функция массива, так что ее нужно вводить сразу в весь диапазон ячеек F47:U47 ).
При правильном решении числа в строкеF47:U47 должны равняться числам в строке F46:U46 .
Необходимо проследить, чтобы в ячейкахV46 и W28 получились 1 (маршрут вошел в Элисту и маршрут вышел из Сухума).
 Нам обязательно нужно сосчитать, сколько раз каждый город назначен для выезда (
Нам обязательно нужно сосчитать, сколько раз каждый город назначен для выезда (Для контроля въездов-выездов запишем в ячейки строки
При правильном решении числа в строке
Необходимо проследить, чтобы в ячейках
3
Установки OpenSolver для задачи "Маршрут навигатора". Решение.
Для удобства конечные пункты маршрута Элиста и Сухум расположены в начале и в конце таблицы переменных, но, вообще говоря, это не требуется.
В установках OpenSolver-Model можно просто для начального города потребовать, чтобы был только выезд, а для конечного – только въезд. А для остальных – чтобы был и въезд и выезд.
Но в этом случае понадобится написать больше ограничений, потому что диапазоны с одинаковыми требованиями разобьются на две части.
В установках OpenSolver-Model можно просто для начального города потребовать, чтобы был только выезд, а для конечного – только въезд. А для остальных – чтобы был и въезд и выезд.
Но в этом случае понадобится написать больше ограничений, потому что диапазоны с одинаковыми требованиями разобьются на две части.
- Введем данные задачи в OpenSolver-Model:
-
Целевая функция в данной задаче – суммарная длина маршрута. Ее можно подсчитать, умножив голубые ячейки таблицы расстояний на соответствующие желтые
ячейки таблицы переменных и полученные результаты сложить. В MS Excel для этого используют формулу
=СУММПРОИЗВ(F6:V22;F28:V44) . - Будем искать самый короткий маршрут, поэтому потребуем, чтобы значение целевой функции было минимальным.
- Переменные в задаче - это желтое поле в таблице переменных.
- Для решения задачи требуется минимальное количество ограничений. Введем их:
-
Число выездов должно быть равно числу въездов:
$F$46:$U$46 = $F$47:$U$47 - Маршрут должен выйти из Сухума:
$W$28 = 1 - Маршрут должен войти в Элисту:
$V$46 = 1
-
Число выездов должно быть равно числу въездов:

Очень важно, что не требуется задавать целочисленные ограничения, так как в классической задаче о назначениях целые решения получаются автоматически
при работе стандартного симплекс-метода оптимизации. Это очень сильно ускоряет расчет и делает его более надежным.
В итоге получаем следующий кратчайший маршрут длиной 902 км.
На карте он будет выглядеть так:
4
Модификация задачи "Маршрут навигатора".
Обычные требования на заход в какие-то определенные города реализуются очень легко. Нужно добавить ограничение, что число выездов или въездов в данный город равно 1.Например, требование на заход в город Минеральные Воды реализуется добавлением в установки OpenSolver-Model условия
Оптимальный маршрут при этом удлиняется до 1007 км и проходит через Кутаиси.
Если, напротив, в какой-то город заходить не следует, например, в Армавир, то в установки OpenSolver-Model добавляем условие
Получим новый маршрут протяженностью 923 км.
Последние пару лет снова активно обсуждается проект восстановления старой Военно-Сухумской дороги, которая соединяла Черкесск и Сухум напрямую через горный хребет. При этом длина дороги должна составить примерно 335 км.
Добавим в таблицу расстояний участки Черкесск-Сухум и Сухум-Черкесск для симметрии с длиной 335 км.

 Скачать файл "03 route Sukhum-Elista.xlsx" (примерно 125 Кб)
Скачать файл "03 route Sukhum-Elista.xlsx" (примерно 125 Кб)