После старта надстройки "Моделирование Монте-Карло" в меню MS Excel «Вставка функций» появится новая группа функций с префиксом "fmc_..." — это генераторы случайных чисел разного вида.
Возвращает натуральное число с равномерным распределением от 0 до 1.
Генератор не имеет параметров и является основой других генераторов. С его помощью получают другие, более изощренные распределения. Этот генератор работает быстрее всех остальных.
Генератор fmc_Rand() полный аналог стандартного генератора случайных числе MS Excel = СЛЧИС (..).
Обратите внимание на скорость работы генераторов и других функций при моделировании.
Надстройка "Моделирование Монте-Карло" всегда показывает время расчета. На это время следует ориентироваться при увеличении статистики.
Если статистика увеличивается в 100 раз, то время расчета увеличивается тоже в 100 раз.
Возвращает случайное число с равномерным распределением от Left до Right.
Генератор fmc_Uniform легко получить из генератора fmc_Rand. Для этого нужно растянуть значения генератора fmc_Rand до интервала Right - Left и сместить до Left. При этом безразлично, в каком порядке показать концы интервала Left и Right - генератор будет работать корректно.
Генератор случайных чисел fmc_Uniform ( Left; Right ) аналогичен генератору
=СЛУЧМЕЖДУ (нижн_граница; верхн_граница) из библиотеки MS Excel, который становится доступен только при подключенной стандартной надстройки "Пакет анализа".
Быстродействие генератора fmc_Uniform ( ) очень близко к быстродействию fmc_Rand ().
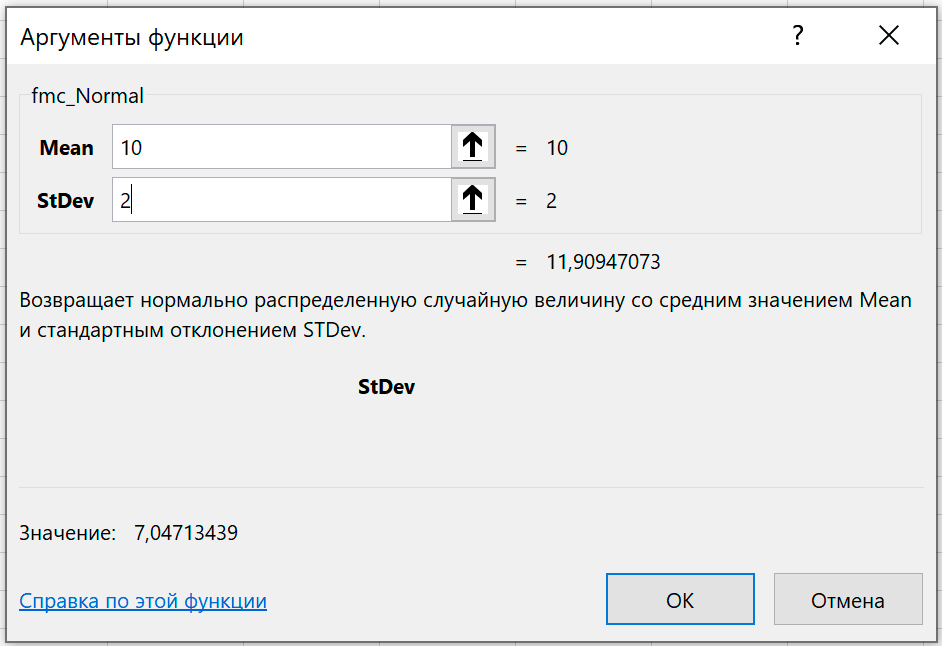
Возвращает нормально распределенную случайную величину со средним значением Mean и стандартным отклонением STDev.
Нормальное распределение - это второе фундаментальное распределение, которое очень часто встречается в нашей жизни.
Параметры распределения вводят числами или ссылками на ячейки.

| A | |
|---|---|
| 1 | = fmc_Normal (10; 5) |
| 2 | = ЕСЛИ ( A1 < 0; 0; A1) |
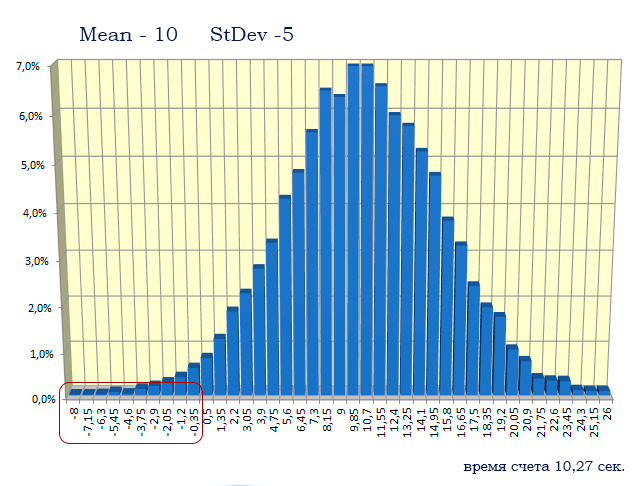
Теперь гистограмма будет выглядеть следующем образом:
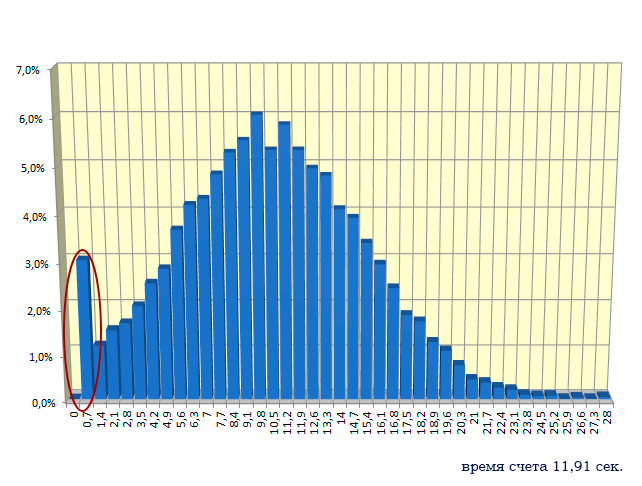
Быстродействие генератора случайных чисел fmc_Normal примерно в
Возвращает дискретную случайную величину с заданным частотным распределением: Values — Probabilities.
Во многих случаях невозможно (или нет смысла) установить конкретный вид функции распределения случайной величины. Чаще всего это связано с малым числом возможных исходов. Однако, если известны вероятности всех возможных исходов, можно моделировать случайную величину по таблице с помощью генератора fmc_Discrete().
| A | B | |
|---|---|---|
| 1 | Values | Probabilities |
| 2 | -10 | 35% |
| 3 | 10 | 60% |
| 4 | 50 | 5% |
Вызываем функцию fmc_Disсrete и показываем, что выигрыши Values содержатся в ячейках A2:A4, а вероятности Probabilities в ячейках B2:B4.
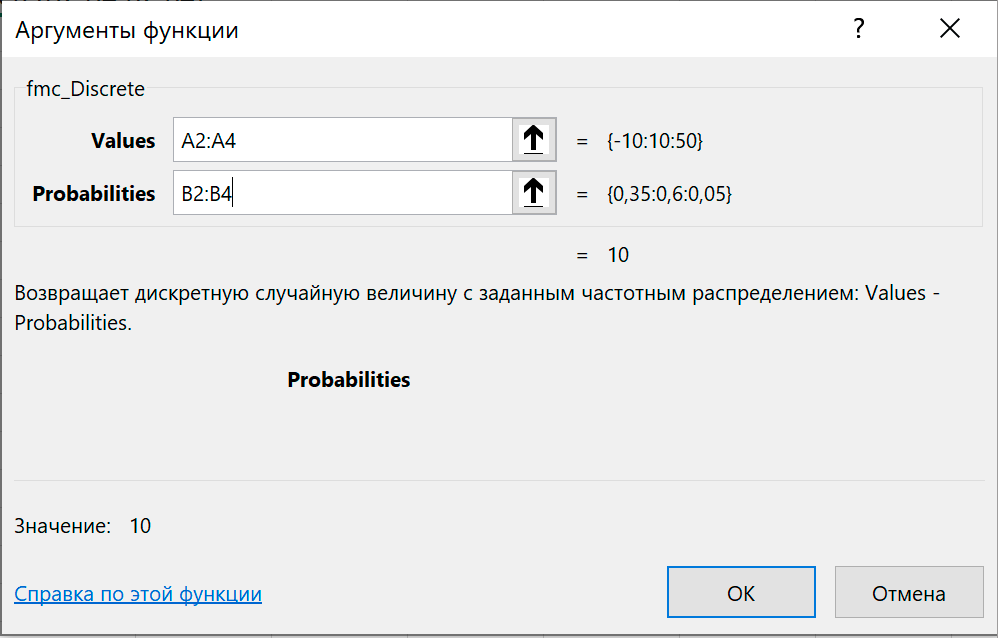
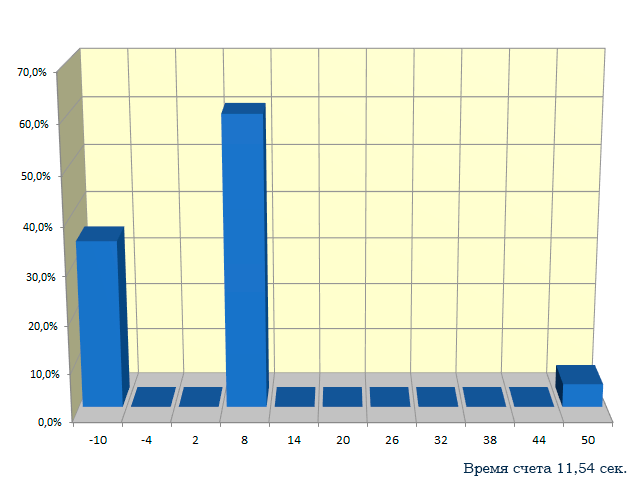
Таким образом, проведено тестирование генератора случайных чисел fmc_Discrete. Полученое распределение полностью соответствует условию задачи.
Генератор fmc_Discrete работает примерно вдвое медленнее генератора fmc_Rand.
Если таблица Values — Probabilities содержит много разрядов, то генератор работает очень медленно.
Возвращает случайную величину времени расходования запаса Inventory при среднем потреблении Mean и стандартном отклонении спроса StDev.
Этот генератор разработан автором сайта для моделирования систем управления запасами и может быть использован для оценки риска дефицита при заданном уровне безопасного резерва (safety stock), для расчета потерь из-за дефицита и для определения оптимального риска дефицита. На сайте есть пример подобного использования генератора.
Предполагается, что спрос клиентов распределен нормально (как это и бывает в подавляющем большинстве случаев).
| A | B | C | |
|---|---|---|---|
| 8 | Invetory | Mean | StDev |
| 9 | 500 | 50 | 10 |
Вызываем функцию fmc_ExhaustTime и показываем, что запас Inventory нужно взять из ячейки A9, средний спрос Mean из ячейки B9, а стандартное отклонение спроса StDev из ячейки C9.
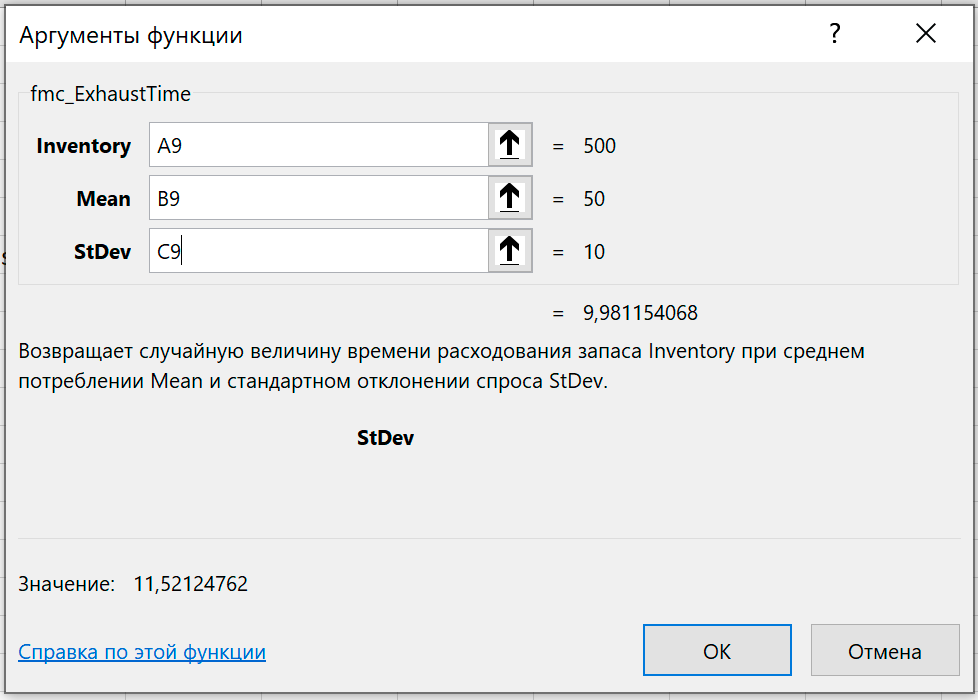

При нормально-распределенном спросе время исчерпания запаса также будет иметь нормальное распределение.
Скорость расчета с генератором fmc_ExhaustTime примерно в 10 раз меньше, чем с fmc_Rand, что неудивительно, учитывая многократный вызов генератора fmc_Normal для моделирования спроса.
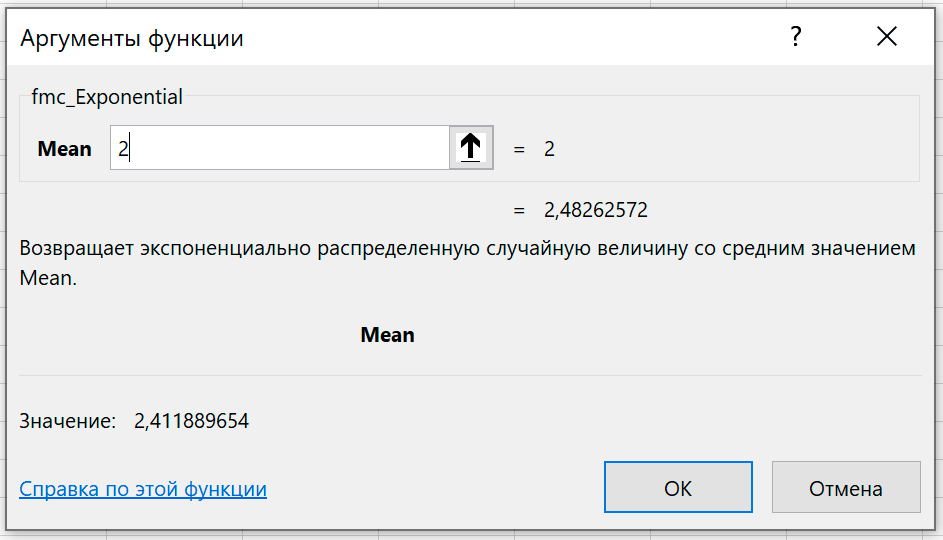
Возвращает экспоненциально распределенную случайную величину со средним значением Mean.
Формула плотности распределения для данного экспоненциального распределения классическая:
p(t) = 1/m * exp(-1/m * t)
Напомним, что при этом среднее значение < t > (Mean) для экспоненциально распределенной случайной величины равно как раз: Mean = < t > = m, как и стандартное отклонение: σ = m.
Аргумент функции можно задать числом или ссылкой на ячейку.
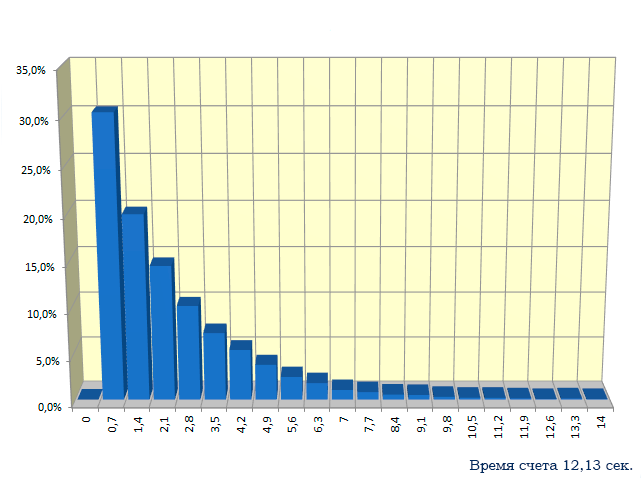
Это распределение широко применяется в теории массового обслуживания, где обычно время обслуживания клиентов принимается распределенным экспоненциально.
Возвращает случайную величину с пуассоновским распределением со средним значением Mean.
Распределение Пуассона дает вероятность того, что за единицу времени произойдет ровно n событий.
Например, вероятность того, что за единицу времени, соответствующую единице измерения потока λ= Mean, в систему поступит заданное количество заявок.
Формула для плотности распределения:
p(n) = e -λ λn /n!
Среднее значение < n > для пуассоновски распределенной случайной величины равно
Mean = < n > = λ, а стандартное отклонение: σ = λ1/2.
Аргумент функции можно задать числом или ссылкой на ячейку.
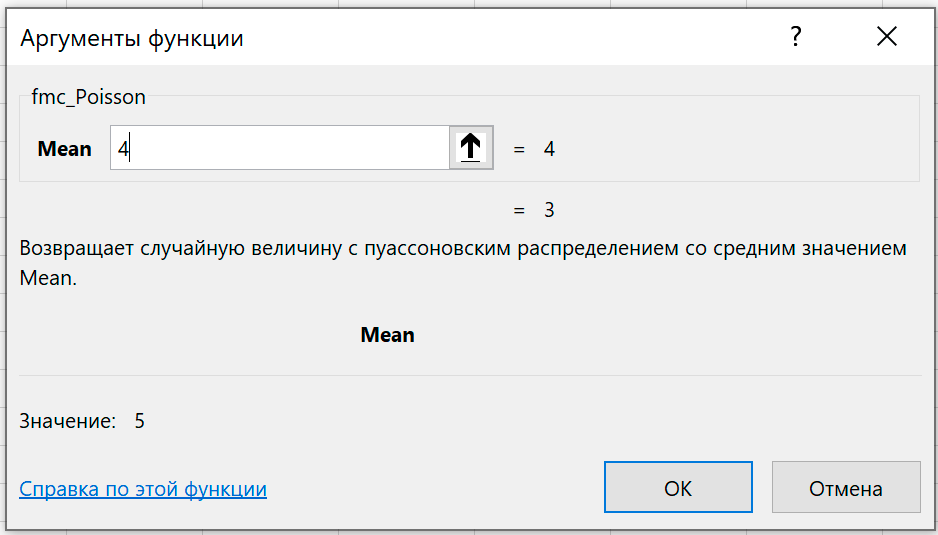


Это распределение широко применяется в теории массового обслуживания. Таким распределением моделируют входной поток независимых клиентов.
Возвращает случайную величину с бета-распределением, приведенным к интервалу от T_min до T_max и максимумом при T_most_probable.
Такое распределение используется при оценке рисков в управлении проектами в модели PERT ( Project Evaluation and Review Technique ).
Плотность вероятности для случайной величины Beta_PERT приблизительно соответствует формуле
 Это распределение получено из стандартных формул для бета-распределением
Это распределение получено из стандартных формул для бета-распределением
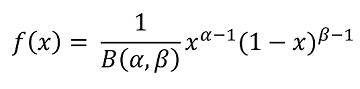 где
где
 путем линейного масштабирования.
путем линейного масштабирования.
При этом среднее значение случайной величины равно
< x > = ( T_min + 4 * T_most_probable + T_max ) / 6,
а стандартное отклонение
s = ( T_max - T_min ) / 6.
Аргумент функции можно задать числом или ссылкой на ячейку.
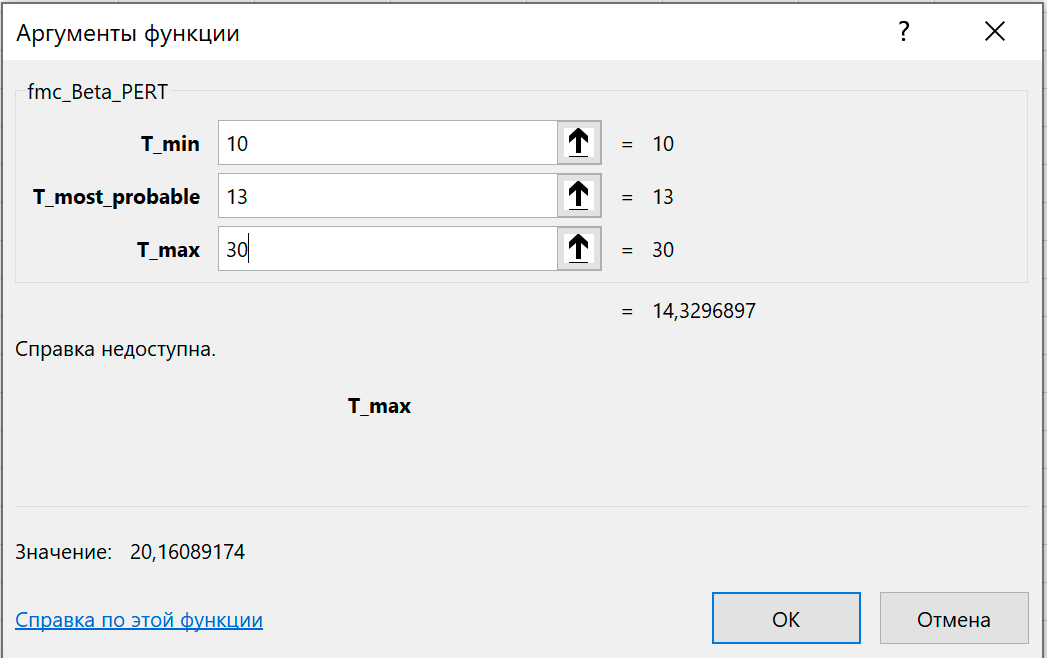
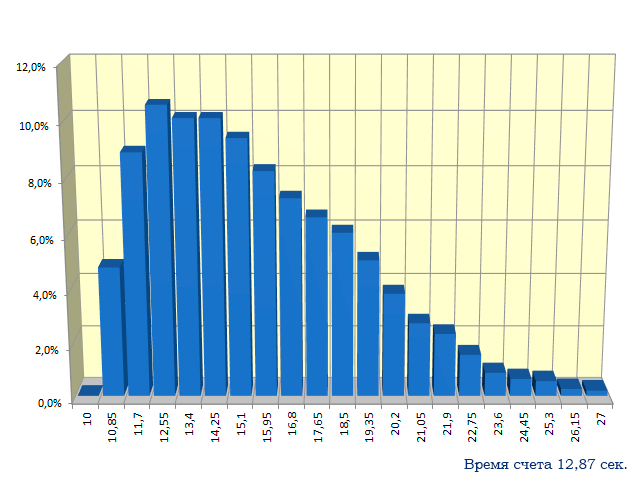
Можно проверить, что среднее значение и стандартное отклонение сгенерированной величины равны оцененным по формулам.

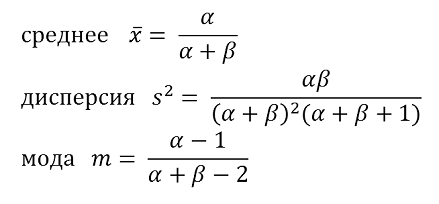
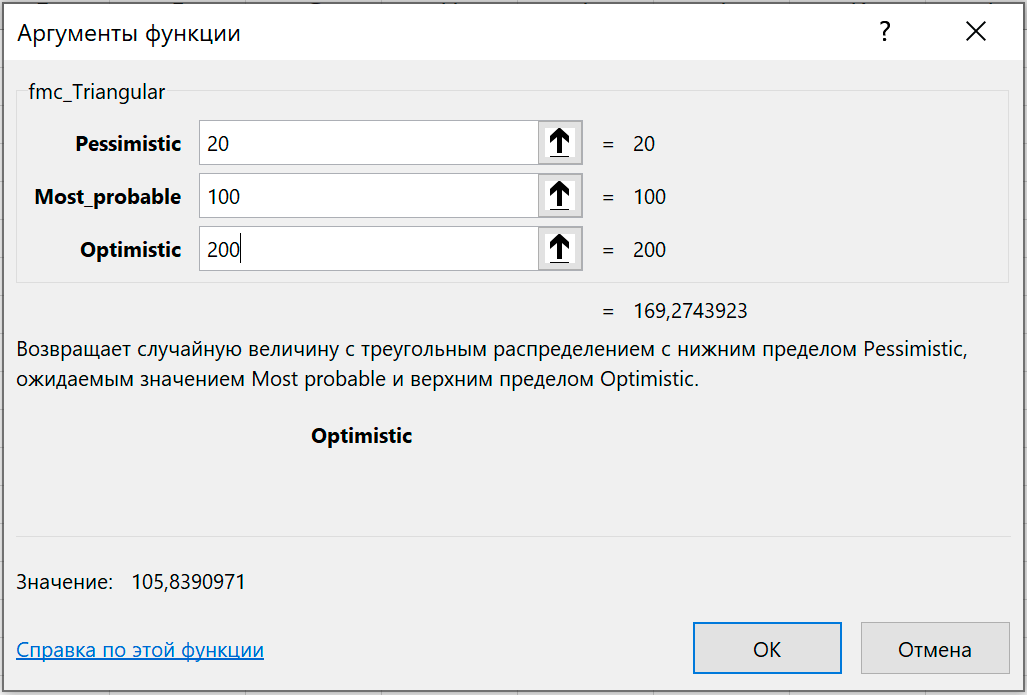
Возвращает случайную величину с треугольным распределением с нижним пределом Pessimistic, ожидаемым (наиболее вероятным) значением Most probable и верхним пределом Optimistic.
Это простое и ясное распределение, которое неплохо, пусть и грубо, имитирует, например, нормальное распределение для целей моделирования поведения систем или же распределение Пуассона.
Аргумент функции можно задать числом или ссылкой на ячейку.