

При открытии файла появится сообщение об опасности макросов. Ответьте «Включить макросы» (вся рабочая часть надстройки и есть макросы, т.е. программа на языке VBA).
После запуска файла в MS Excel появится панель управления надстройкой:

Работа с надстройкой начинается с блока "Метод расчета". Здесь имеется два флажка, выбор одного из которых полностью меняет работу надстройки.
При выборе Формулы ТМО надстройка расчитывает параметры систем массового обслуживания по известным формулам теории массового обслуживания. Достаточно выбрать вид СМО и ввести ее параметры и надстройка рассчитает все характеристики системы, которые возможно рассчитать в теории.
При выборе МК - моделирование появится другая панель. МК - моделирование используетя для расчета параметров систем массового обслуживания с помощью простейшего статистического моделирования характеристик в случае, когда требования теории к функции распределения потоков клиентов или обслуживания не удовлетворяются.
После выбора Формулы ТМО на панели интерфейса надстройки необходимо отметить все параметры системы массового обслуживания, которую нужно проанализировать.
Для запуска надстройки нажмите на клавишу Рассчитать:

Сводка результатов расчетов отображается на листе Excel. Для данных, выбранных на панели надстойки итоговый отчет имеет вид:
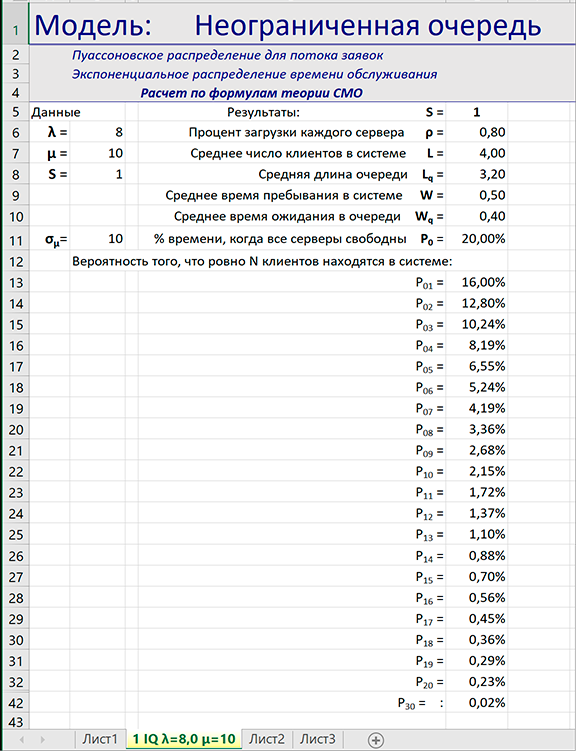
Компания планирует поставить аппарат по продаже напитков, закусок и кофе в торговом центре. Она оценивает поток клиентов 8 человек в час. В среднем автомат тратит 6 минут на обслуживание каждого клиента. Предполагая пуассоновский поток заявок и экспоненциальное распределение для времени обслуживания найти: a. Долю времени, когда автомат загружен; b. Долю времени, когда он бездействует; c. Среднее число клиентов у автомата; d. Среднее число клиентов в очереди у автомата; e. Среднее время, затрачиваемое клиентом для получения денег; f. Среднее время, которое клиент проводит в очереди; g. С какой вероятностью возле автомата будут стоять более 3 клиентов.
Программа требует ввода трех характеристик - λ , μ и S :
λ - интенсивность входного потока (среднее число клиентов,
приходящих в систему за единицу времени).
Предполагается пуассоновский входной поток - при этом поступление
клиентов в систему независимое, а время между поступлениями заявок
распределено экспоненциально.
Значение λ можно ввести как натуральное, десятичное и даже дробное
числа в формате
μ - средняя скорость, с которой каждый сервер может обслуживать
клиентов. Иначе – среднее число клиентов, которых сервер может
обслужить в единицу времени, или пропускная способность сервера (если
он загружен на 100%). Функция распределения для потока обслуживания
тоже экспоненциальная.
Значение μ можно ввести как натуральное, десятичное и даже дробное
числа в формате a/b. Но нельзя вводить смешаное число!
Если величина введенного числа выходит за допустимые смысловые
границы, которые устанавливает модель для данного входного параметра,
программа выдает предупреждающее сообщение и требует изменить ввод.
S - количество серверов. В модели предполагается, что все
серверы совершенно одинаковы, т.е. среднее время обслуживания клиентов
строго одинаково, а функция распределения времени обслуживания
экспоненциальная у всех серверов. (Технический предел числа серверов -
30.)
Формат S натуральное число, меньше 31. Если нужно сравнить
характеристики системы при нескольких значениях S, можно задать
интервал значений количества серверов, например: 1-5 или 4-10. В
результате вы получите сводную страничку характеристик.
При выборе МК - моделирование появится новая панель интерфейса надстройки.

Надстройка готова выполнить статистическое моделирование (моделирование
методом Монте-Карло ).
Для ввода параметров статистики добавлен блок
"Статистика моделирования". Надстройка позволяет использовать
не экспоненциальные распределения потоков клиентов или обслуживания, а
Бета-распределение.
ΔTmin - минимальный интервал времени между заявками клиентов
ΔTλ - наиболее вероятное время между посуплениями заявок клиентов
ΔTmax - максимальный интервал времени между заявками клиентов.
При его определением необходимо исключить заявки при форс-мажорных
обстоятельствах.
ΔTmin - минимальное время обслуживания клиентов в системе
ΔTμ - наиболее часто встречающееся время обслуживания клиентов
ΔTmax - максимально наблюдаемое время обслуживания клиентов.
При его определении необходимо исключить обслуживание при
форс-мажорных обстоятельствах.
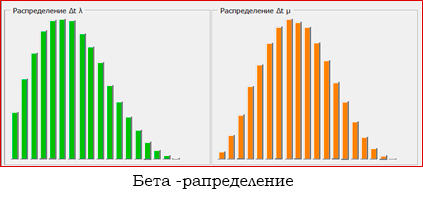
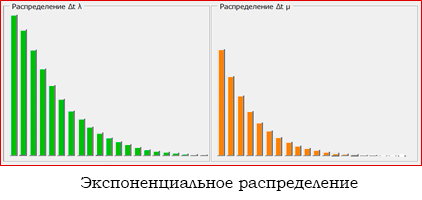
Статистика моделирования. Так как моделирование всегда начинается
с пустой системы без обслуживающихся клиентов, то выход модельной
системы на стационарное состояние занимает некоторое заранее неизвестное
время. Ввиду этого цепочка моделируемых событий не должна быть слишком
короткой. Значение по умолчанию (1000 единиц времени) чаще всего вполне
подходит. Однако имеет смысл посмотреть, не отличаются ли результаты
моделирования при более длинной заданной цепочке.
Параметр Число опытов" задает количество повторений моделирования
цепочки событий. Чаще всего с учетом практически требуемой точности
моделирования достаточно 100 повторений. Так как время моделирования (в
сек) указано в результатах расчета, всегда можно сориентироваться, не
приведет ли увеличение задаваемой статистики к неприемлемо длительному
расчету.
При выборе чекбокса Ограниченная очередь в панели надстройки появится новый блок Длина очереди.

Программа требует ввода четырех характеристик - λ, μ, S и N.

N - максимально возможная длина очереди (ограничение либо
техническое, либо психологическое).
Параметр определяет количество клиентов (сверх тех, кто уже
обслуживается серверами), которое будет поставлено системой в очередь
на обслуживание.
Если поступающий клиент сталкивается с очередью
максимальной заданной длины, он отвергается системой без обслуживания,
что позволяет говорить о потерянных клиентах, которых при
неограниченной очереди нет в принципе.
При выборе МК - моделирование в интерфейсе надстройки появляется блок Длина очереди.

Программа требует ввода от четырех характеристик до восьми характеристик - λ (или ΔTmin, ΔTλ и ΔTmax) , μ (или ΔTmin, ΔTμ и ΔTmax), S и N, если используются не экспоненциальные распределения потоков клиентов или обслуживания.
В задачах СМО "Ограниченная очередь" требование μ*S <= λ, т.е. входной поток больше суммарного потока обслуживания, не работает. Входной поток может быть больше суммарного потока обслуживания, и программа в этом случае выполнит расчет.
При выборе чекбокса Ограниченная популция в панели надстройки появится новый блок Популяция клиентов.

Программа требует ввода четырех характеристик - λ, μ, S и K.

K - размер популяции.
Число потенциальных клиентов, которые могут подать заявку на
обслуживание. Максимальное значение K=50.
Очевидно, что S <= K. Так как при S > K часть серверов
никогда не работает.
Так же, что при μ*S <= λ*K система обслуживания не справляется с
потоком заявок. Надстройка в этом случает выдаст сообщение об ошибке.

Программа требует ввода от четырех - λ , μ, S и K - до восьми характеристик: Блок Поток заявок ΔTmin, ΔTλ, ΔTmax, Блок Поток обслуживания ΔTmin, ΔTμ, ΔTmax, S и K (если используются не экспоненциальные распределения потоков клиентов или обслуживания).
 Скачать надстройку "Системы массового обслуживания" (примерно 180
кб)
Скачать надстройку "Системы массового обслуживания" (примерно 180
кб)