Ситуация: Далекая мишень.
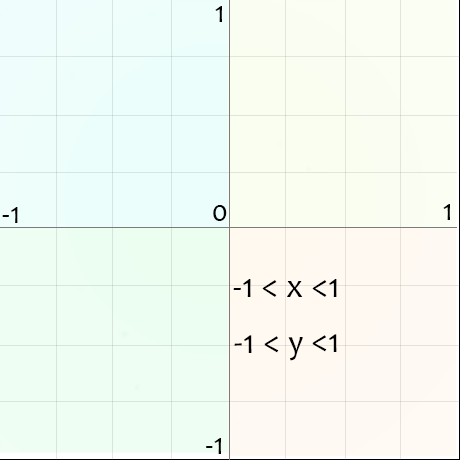
Мишень - это черная квадратная рамка со стороной 2 дм, напечатанная на стандартном листе бумаги А4.
Наша задача – просто попасть в мишень. Промахи случаются гораздо чаще попаданий, ввиду значительного расстояния до мишени. Бросаем дротики до 100 попаданий в мишень.
При попадании дротика в мишень в ней остаются маленькие отверстия от иглы, так что по завершении игры отлично видно, куда попадали дротики. В силу случайности попаданий отверстия расположены хаотично.

- Сколько примерно попаданий будет в правый верхний квадрант (или любой другой квадрант на выбор), если общее количество отверстий от дротиков N равно 100? Почему?
Можно ли записать общую формулу для вычисления числа попаданий? - Будет ли реальное число попаданий в выбранный квадрант точно равно предвычисленному?
Как сильно может отличаться от ожидаемого реальное число попаданий в выбранный квадрант?
1
Постановка задачи статистического моделирования с помощью физической модели.
Моделирование ситуации Далекая мишень
Как имитировать случайное попадание дротика в мишень? И вообще получить число случайно?
Алгоритм
построения модели Далекая мишень

Работающая модель
- Здесь можно поэксперементировать с работающей моделью:
- сделать ряд одиночных выстрелов;
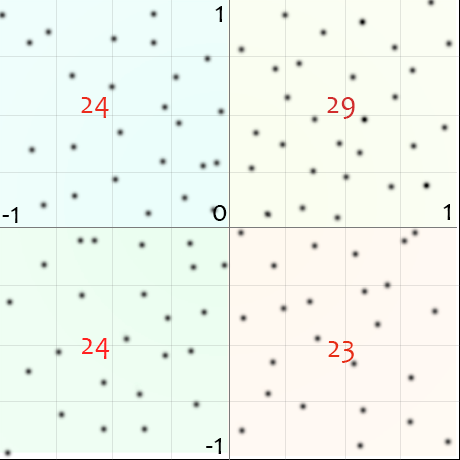
- произвести целую серию выстрелов с попаданием 100 игл в мишень и посмотреть, сколько игл попадает в каждый из квадрантов.
- Число попаданиий в
I квадрант: 0 - Число попаданиий в
II квадрант: 0 - Число попаданиий в
III квадрант: 0 - Число попаданиий в
IV квадрант: 0
Подготовить поле на листе Excel
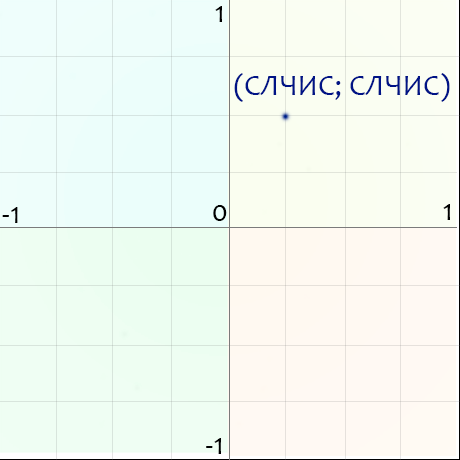
Подготовим диаграмму для визуализации данных.В поле диаграммы будем строить точки из таблицы, в которой датчиком случайных чисел генерируется два числа:

Функция-генератор случайных чисел СЛЧИС() ( англ. Rand() )
Случайное число получают с помощью генератора случайных чисел.В Excel таким генератором является функция без аргументов
Вероятности появления любого числа из этого диапазона совершенно одинаковы, т.е. числа близкие к 0, к 0.5 или к 1 появляются с равной частотой. Функция использует специальный алгоритм для генерации длинной цепочки случайных чисел.
Если ввести функцию
- Примерный код функции СЛЧИС()
- (
iseed – начальное значение генератора – произвольное, желательно большое, целое число,4.6566128752458E-10 = 1/2147483647, 2147483647 = 231 - 1 )
a = 16807 * iseed b = a - 2147483647 * Int(a * 4.6566128752458E-10) iseed = b СЛЧИС = b * 4.6566128752458E-10
Использование функции СЛЧИС() для определения координат точки попадания
Введем в ячейки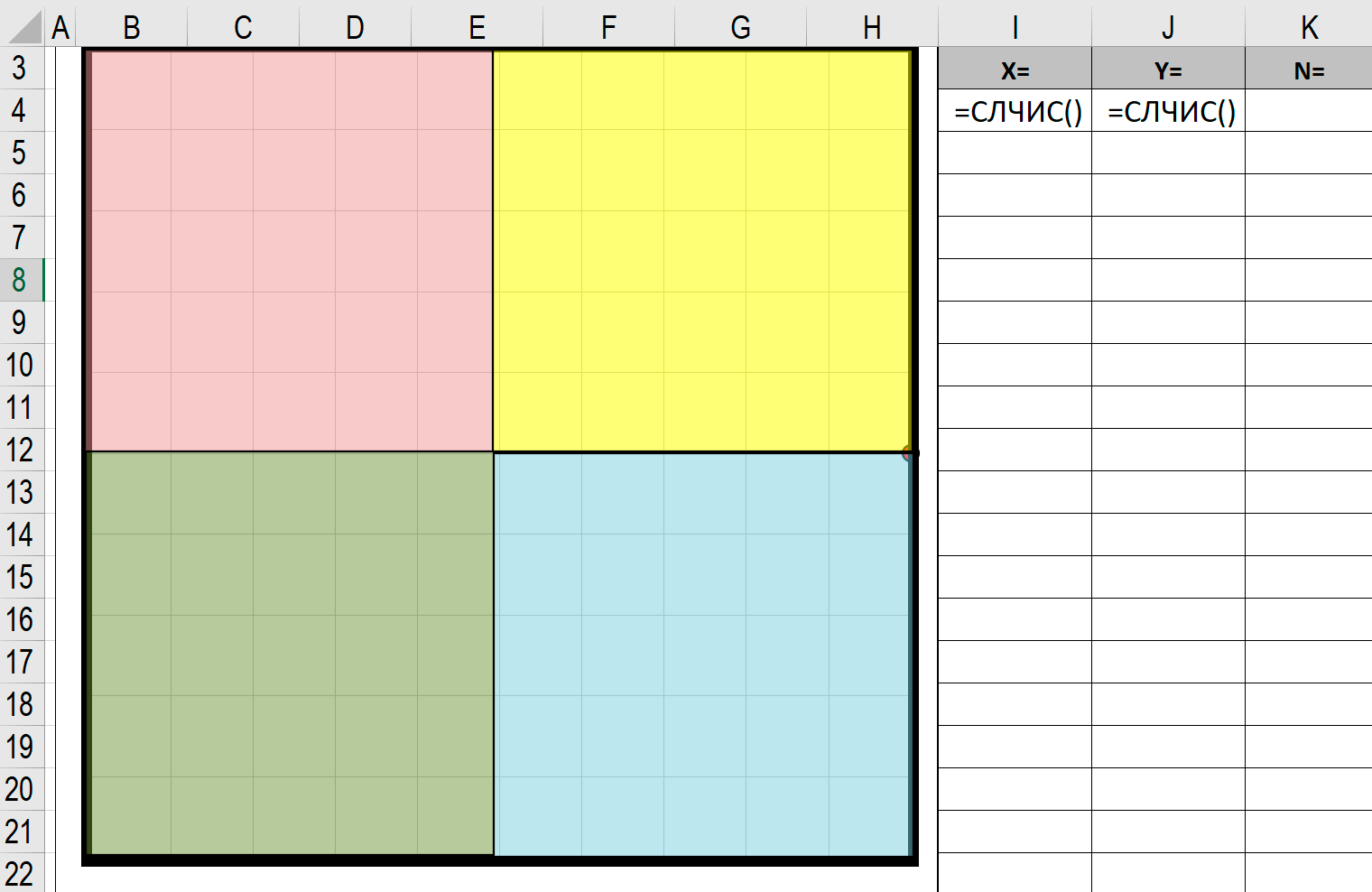 Протянем формулы вниз, и увидим на диаграмме точки попадания дарта в мишень.
Протянем формулы вниз, и увидим на диаграмме точки попадания дарта в мишень. 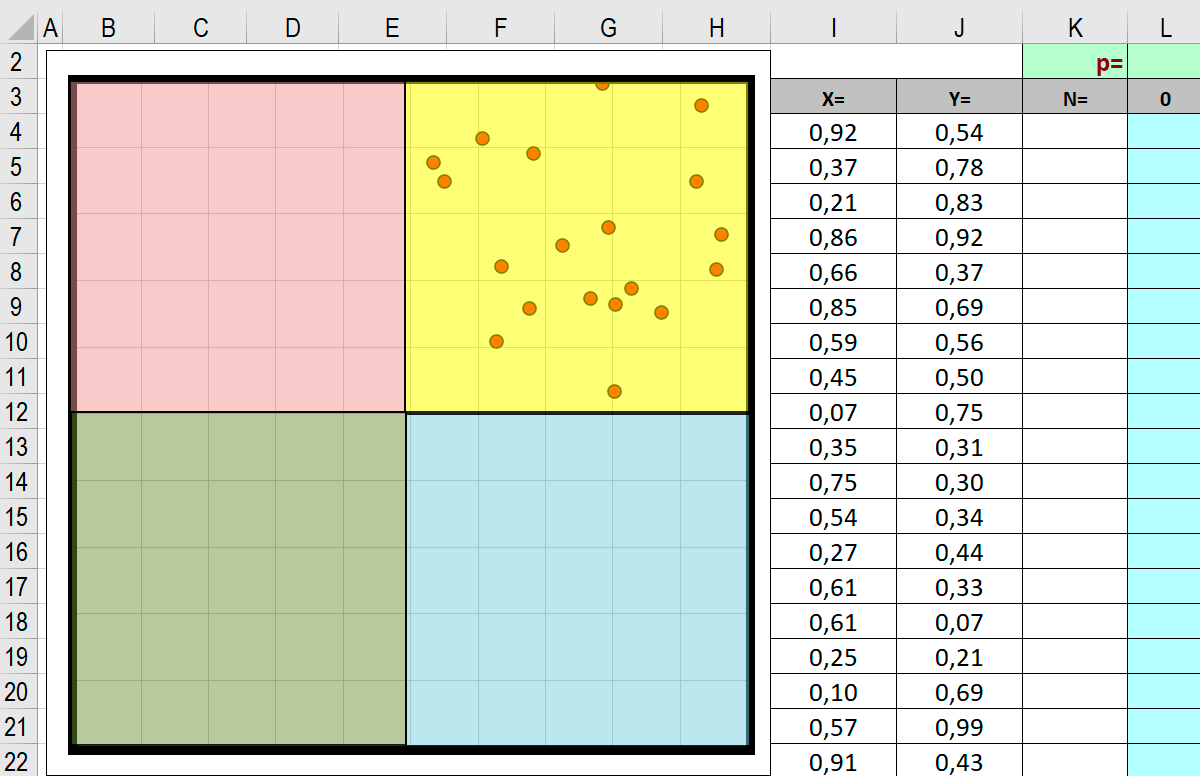
Почему модельный дротик все время попадает в верхний правый квадрант?
Вспомним, что функция- Поэтому для того, чтобы получить случайное число, изменяющееся от -1 до 1, необходимо
- случайное число
ξ , сгенерированное функциейСЛЧИС() умножить на2 :
2 * ξ , - а затем из модифицированного случайного числа
2 * ξ вычесть 1:2 * ξ - 1 .
- Тогда координаты попадания в квадратную мишень со стороной 2 дм нужно моделировать как
-
X = 2 * ξ - 1 -
Y = 2 * ξ - 1 - Запишем формулу
= 2 * СЛЧИС() - 1 в ячейкиI4 иJ4 .
Как смоделировать 100 попаданий?
Для того, чтобы смоделировать сразу N=100 попаданий, протянем формулы из ячеек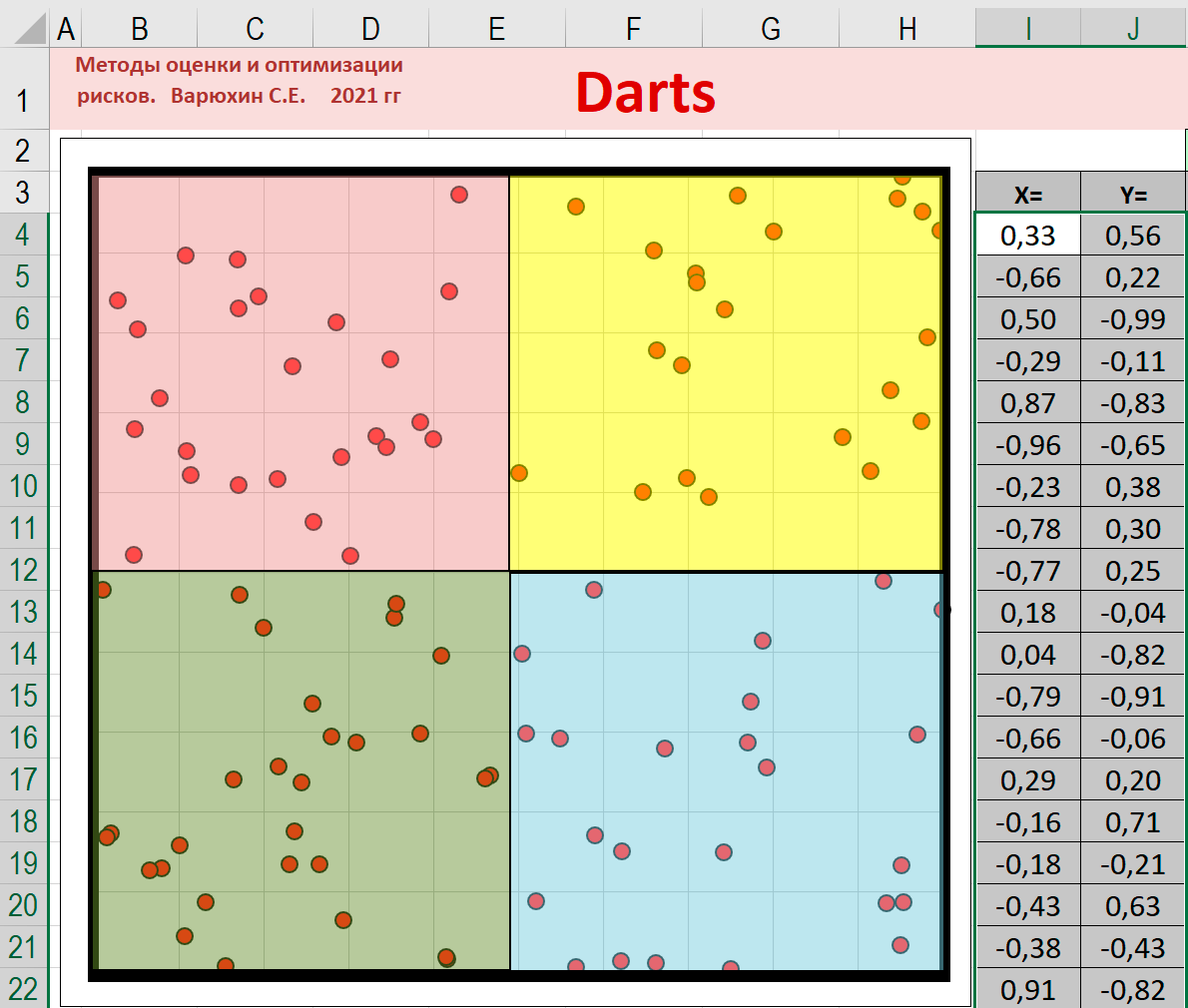
Подсчет попаданий дротика в заданный квадрант
Подсчитаем количество попаданий в верхний правый квадрант.Условие попадания:
Для того, чтобы выделить точки, попавшие в верхний правый квадрант, присвоим им маркер
если значение ячейки
В ячейке
 Скачать файл "21 Darts.xlsx" (примерно 776 Кб)
Скачать файл "21 Darts.xlsx" (примерно 776 Кб)
- Этот файл содержит:
- рабочую модель с выстрелом из 100 игл.
- рабочую модель с выстрелом из 400 игл.
- рабочую модель с выстрелом из 1600 игл.
- рабочую модель с выстрелом из 6400 игл.
2
Как оценить ожидаемое число событий и дисперсию.
Как оценить, какое количество попавших в мишень дротиков попадет именно вВспомним основные формулы из теории вероятности.
если обозначить через
- В нашем случае:
- вероятность попасть в определенный квадрант - 1/4 (так как квадрантов 4)
p = 1/4 - так как по условию в мишень попали 100 раз, то
N = 100 - ожидаемое количество попаданий в выбранный квадрант
‹n›= 100 * 1/4 = 25 - вероятность не попасть в определенный квадрант - 3/4
q = 3/4 - дисперсия
‹Dn›= 100×1/4×3/4 = 18,75 - cтандартное отклонение
‹sn›= 18,75½ = 4,33
Итак, ожидаемое количество попаданий в выбранный квадрант: 25±4,33
Какой разброс числа попаданий от ожидаемых 25-ти мы можем получить?
- Для начала ответим на вопросы.
- Каким вообще может быть число попаданий в заданный квадрант?
Практически каждый ответит на него: от0 до100 .
И действительно, нет никаких причин, запрещающих игроку, специально не целящегося в определенное место мишени, 100 раз подряд попасть в заданный квадрант. Так же как нет причин для него все 100 раз промахнуться!
Однако на практике мы этого НИКОГДА НЕ НАБЛЮДАЕМ! - С какой вероятностью дротик не попадет в заданный квадрант?
- Не трудно посчитать.
- Вероятность не попасть в заданный квадрант - 3/4 или 0,75
- Вероятность не попасть в заданный квадрант за два броска - 3/4×3/4 или (3/4)2, а это 9/16 или ≈0,56
- Вероятность не попасть в заданный квадрант за три броска - 3/4×3/4×3/4 или (3/4)3, а это 27/64 или ≈0,42
- Вероятность не попасть в заданный квадрант за сто бросков - (3/4)100, а это ≈3,2×10-13 или
0,00000000000032 , т.е. почти 0.
-
С какой вероятностью дротик попадет в заданный квадрант?
- Вероятность попасть в заданный квадрант - 1/4 или 0,25
- Вероятность попасть в заданный квадрант два раза подряд - 1/4×1/4 или (1/4)2, а это 1/16 или ≈0,06
- Вероятность попасть в заданный квадрант три раза подряд - 1/4×1/4×1/4 или (1/4)3, а это 1/64 или ≈0,015
- Вероятность попасть в заданный квадрант все сто раз - (1/4)100, а это ≈6,2×10-61, т.е. 0.
- Итак,
- вероятность выпадения определенного события не меняется (в нашем случае вероятность для дротика попасть в заданный квадрант все время 1/4);
- вероятность многократного повторения ОДНОГО И ТОГО ЖЕ определенного события с увеличением количества испытаний уменьшается. Поэтому вероятность при 100 бросках все время попадать в заданное место (1/4)100, т.е.
Cколько дротиков может попасть в заданный квадрант при проведении нескольких серий испытаний?
Для ответа на этот вопрос обратимся к частотной диаграмме.
- Для построения частотной диаграммы возьмем две оси:
- на одной оси отложим возможные результаты нашего эксперимента
ось
‹n›
как мы предпалагаем, это цифры от 0 до 100 - на другой оси
k - количество результатов, выпавших при проведении испытания
Выпавший результ изобразим в виде маленького красного прямоугольника. Если выпадает один и тот же результат в разных опытах,
то на диаграмме один красный прямоугольник встанет на другой.
Чем выше пирамида из прямоугольников, тем чаще выпадает этот результат при проведении испытаний.
Частотная диаграмма числа попаданий в I квадрант.
Число испытаний:
Распределение числа игл, попавших в первый квадрант на частотной диаграмме.
Задайте число испытаний: 100, 1000, 10000.
Чем больше число испытаний, тем ближе функция распределения нашей случайной величины (число попаданий в заданный квадрант) к нормальной функции распределения.
Таким образом, уже при 10 тыс. испытаний мы наблюдаем иллюстрацию Центральной предельной теоремы теории вероятности.
Центральная предельная теорема
Сумма большого числа примерно одинаковых случайных величин с произвольными функциями распределения всегда имеет приблизительно нормальную функцию распределения.
И чем больше наблюдений будет в нашем распоряжении, тем более точно мы сможем оценить величину
среднего значения числа попаданий
Закон больших чисел
Закон больших чисел утверждает, что при бесконечном увеличении числа наблюдений ошибка в расчете среднего значения
Δ
- Итак, что мы сделали?
- Построили по ситуации «Далекая мишень» математическую модель с использованием ГЕНЕРАТОРА СЛУЧАЙНЫХ ВЕЛИЧИН.
- Многократно обсчитали эту модель:
- находили среднее число попаданий в заданный квадрант
- вычисляли стандартное отклонение
- На основе полученных многократных вычислений определили вероятностные характеристики рассматриваемого процесса. По сути мы применили метод Монте-Карло.
3
Применение надстройки Монте-Карло для статистического моделирования
- Подключите надстройку "Моделирование Монте-Карло".
- Откройте файл "21 Darts.xlsx", который был описан на раскрывающейся панели Моделирование ситуации Далекая мишень в рабочей книге MS Excel или создайте свою модель в рабочей книге MS Excel.
-
Введите в поле Целевые ячейки ячейку,в которой вычисляется число попаданий в
I квадрант.
В нашем случае, это ячейкаK2 .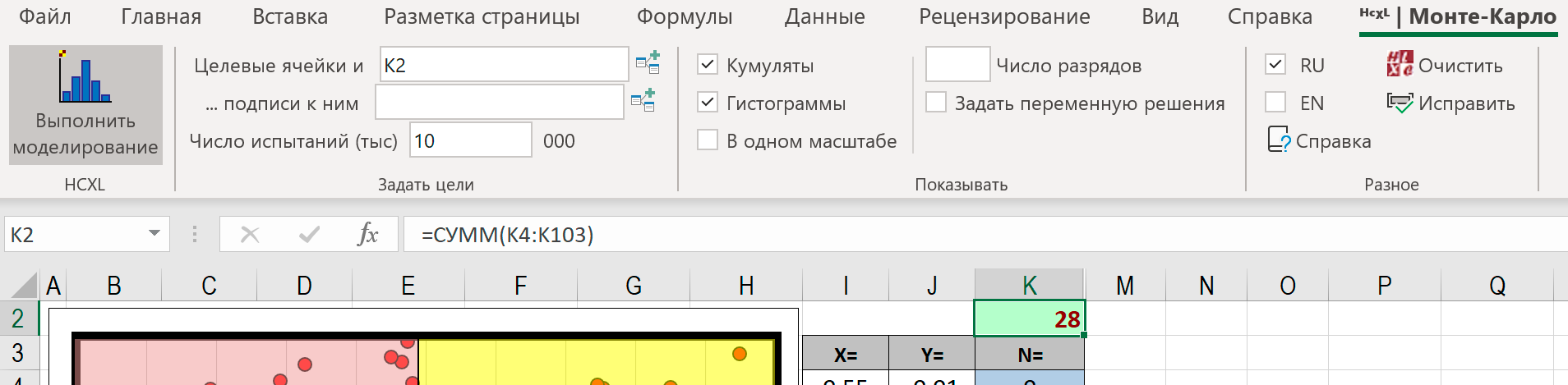
- Запустите надстройку, нажав кнопку Выполнить моделирование.

- Надстройка
- провела 10 тысяч испытаний;
- вычислила среднее значение - 25;
- нашла стандартное отклонение при вычислении средней величины - 4,33;
- вычислила ошибку оценки среднего значения при 10 тысячах испытаниях - 0,085;
- вывела максимальное и минимальное значения, которае выпадали при проведении 10 тысяч испытаний;
- вывела медианное значение случайной величины. При следующем запуске надстройки данные будут другими. Так и должно быть, ведь мы моделируем случайные величины.
4
Где используют статистическое моделирование
Рассмотрим простой пример.
А если выбрать не квадрант на нашей мишени, а произвольную фигуру.
Возможно ли оценить ее площадь?
Очевидно, что отношение площади фигуры (Sфигуры) к площади всего поля (Sполя) равно отношению числа попаданий в фигуру (N в фигуру) к общему числу бросков (Nвсего):
где ΔSфигуры - точность вычисления площади фигуры. Эта величина зависит от числа бросков.
Чем больше дротиков мы бросим, тем точнее определим площадь фигуры.
СОМНЕВАЕТЕСЬ?
Тогда вернемся к нашей мишени.
- Возьмем четыре мишени:
- в первую запустим иглы так, чтобы в мишень попали 100 игл;
- во вторую запустим иглы так, чтобы в мишень попали 400 игл;
- в третью запустим иглы так, чтобы в мишень попали 1600 игл;
- в четветрую запустим иглы так, чтобы в мишень попали 6400 игл. Будем вычислять не только общее количество игл, попавших в каждый квадрант, но и их долю.
Фактически, данные в процентах показывают отношение площади квадранта к площади всей мишени. Мы ожидаем, что эта величина равна 25%.
Как видим, чем больше игл попадает в мешень, тем точнее результат и меньше разброс в определении площади.
- Теперь используем надстройку Моделирование Монте-Карло и смоделируем 10 тысяч испытаний.
- Введем данные о процентном соотношении доли попаданий в 1 квадрант к общему числу игл.
Обратите внимание, что эти ячейки читают данные с соответствующих листов, на которых с помощью Генератора случайных чисел (функция=СЛЧИС()) ) моделируются попадания
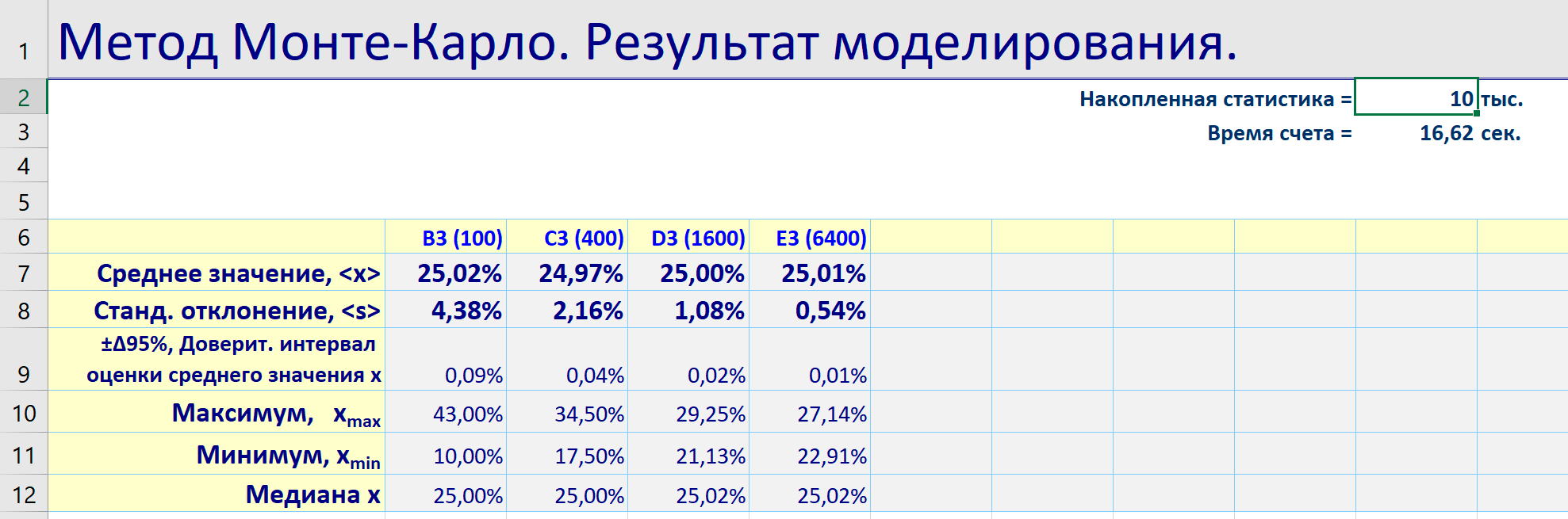
- После запуска надстройки получим файл, на первом листе которого выведены результаты моделирования:
- среднее значение моделируемой случайной величины
- как мы и ожидали, это число близкое к 25%, которое определяется все точнее с увеличением статистики; - стандартное отклонение - это характерный разброс случайной величины, который показывает, на сколько результат единичного опыта отличается от среднего значения;
- доверительный интервал оценки среднего значения - этот параметр показывает ошибку оценки среднего с учетом множества испытаний;
Другими словами, это число показывает, с какой погрешностью определено среднее значение случайной величины. - строка
Максимум показывает, какое максимальное значение при 10 тысячах испытаниях достигала случайная величина - строка
Минимум выводит самое маленькое значение, которое случайная величина достигала при 10 тысячах испытаниях; - сторока
Медиана показывает значение случайной величины в середине интервала. - Если в надстройке была отмечена опция
Гистограммы , то на втором листе файла мы увидим построеные гистограммы, на которых показано, сколько раз средняя случайная величина, которую мы моделировали, принимала то или иное значение:
- среднее значение моделируемой случайной величины
В этой задаче мы моделируем случайную величину, которая показывает, какая доля попавших в мишень игл приходится на первый квадрант.
Обратите внимание, метод Монте-Карло ничего "не знает" ни о мишени, ни о площади квадранта, а работает со случайными числами. Использование этого метода позволяет нам довольно точно определить некое число, которое, как знаем только мы, является площадью квадранта.
И этот факт открывает перед нами большие возможности, так как дает возможность моделировать совершенно разные величины: выручку, спрос, финансовые потоки и т.д.